Problem Set 6

due by 11:59 p.m. on Thursday, April 3, 2025

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

If you have questions while working on this assignment, please come to office hours, post them on Piazza, or email cs112-staff@cs.bu.edu.

Part I

50 points total

Creating the necessary file

Problems in Part I will be completed in a single PDF file. To create it, you should do the following:

1. Open the template that we have created for these problems in Google Docs: ps6_partI

2. Select File->Make a copy..., and save the copy to your Google Drive using the name ps6_partI.

3. Add your work to this file.

4. Once you have completed all of these problems, choose File->Download->PDF document, and save the PDF file on your machine. The resulting PDF file (ps6_partI.pdf) is the one that you will submit. See the submission guidelines at the end of Part I.

Problem 1: More Sorting practice

12 points; 2 points for each part; individual-only

Important: When answering these questions, make sure to apply the versions of these algorithms in the Sort class we give you. The Java code for each algorithm can be found in our Sort class.

Given the following array:

{14, 7, 27, 13, 24, 20, 10, 33}

1. If the array were sorted using selection sort, what would the array look like after the second pass of the algorithm (i.e., after the second time that the algorithm performs a pass or partial pass through the elements of the array)?

2. If the array were sorted using insertion sort, what would the array look like after the fourth iteration of the outer loop of the algorithm?

3. If the array were sorted using the version of bubble sort presented in lecture, what would the array look like after the third pass of the algorithm?

4. If the array were sorted using the version of quicksort presented in lecture, what would the array look like after the first call to the partition() method?

5. If the array were sorted using the version of quicksort presented in lecture, what would the array look like after the second call to the partition() method?

6. If the array were sorted using the version of mergesort presented in lecture, what would the array look like after the completion of the fourth call to the merge() method—the method that merges two subarrays? Note: the merge method is the helper method; is not the recursive mSort method.

Problem 2: More Practice with big-O

12 points total; 4 pts. each part; individual-only

1. Determine the appropriate big-O expression for each of the following functions, and put your answer in the table we have provided in section 2-1 of ps5_partI. We’ve included the answer for the first function. (Note: We’re using the ^ symbol to represent exponentiation.)

   1.     a(n) = 5n + 1
   2.     b(n) = 2n^3 + 3n^2 + nlog(n)
   3.     c(n) = 10 + 5nlog(n) + 10n
   4.     d(n) = 4log(n) + 7
   5.     e(n) = 8 + n + 3n^2

2. In the following code fragment, how many times is the count() method called as a function of the variable n? Use big-O notation, and explain your answer briefly.

   for (int i = 0; i < 2*n; i++) {
       for (int j = 0; j < n - 1; j++) {
           count();
       }
   }
   

3. In the following code fragment, how many times is the count() method called as a function of the variable n? Use big-O notation, and explain your answer briefly.

   for (int i = 0; i < 5; i++) {
       for (int j = 0; j < n; j++) {
           for (int k = n; k > 0; k = k/2) {
               count();
           }
       }
   }
   

Problem 3: Comparing two algorithms

6 points; individual-only

Suppose you want to find the smallest element in an unsorted array of n elements. Below are two possible algorithms for doing so:

Algorithm A:

public static int findMinA(int[] arr) {
    Sort.mergesort(arr);
    return arr[0];
}

Algorithm B:

public static int findMinB(int[] arr) {
    int smallest = arr[0];

    for (int i = 0; i < arr.length; i++) {
        if (arr[i] < smallest) {
            smallest = arr[i];
        }
    }

    return smallest;
}

What is the worst-case time efficiency of algorithm A in terms of the length n of the array? What is the worst-case time efficiency of algorithm B? Use big-O notation, and explain your answers briefly.

Problem 4: Even more practice with sorting - Quicksort

5 points; individual-only

Important: When answering these questions, make sure to apply the versions of these algorithms that are in the Sort class we give you. The Java code for each algorithm can be found in our Sort class.

Given the following array:

{14, 7, 27, 13, 24, 20, 10, 33}

1. If the array were sorted using quicksort, what would the array look like after the third call to the partition method?

2. If the array were sorted using quicksort, what would the array look like after the fourth call to the partition method?

Problem 5: Even more practice with sorting - Mergesort

6 points; 2 points for each part; individual-only

Given the following array:

{24, 3, 27, 13, 34, 2, 50, 12}

1. If the array were sorted using the version of mergesort presented in lecture, what would the array look like after the completion of the second call to the merge() method—the method that merges two subarrays? Note: The merge method is the separate helper method; is not the recursive mSort method.

2. What would the array look like after the completion of the fourth call to the merge() method?

3. The initial call to the recursive mSort() method is made from within the mergeSort() “wrapper” method. This initial call to mSort() is not a recursive call, because the method is not calling itself. Rather, all recursive calls to mSort() are made from within mSort().

   Assuming that the array has at least two elements, the initial invocation of mSort() makes two recursive calls (which in turn lead to other recursive calls, and so on). Starting with the initial array above, what would the array look like after the completion of the first of these two recursive calls?

Problem 6: First Practice with references

9 points total; individual-only

A doubly linked list consists of nodes that include two references: one called next to the next node in the linked list, and one called prev to the previous node in the linked list. The first node in such a list has a prev field whose value is null, and the last node has a next field whose value is null.

The top portion of the diagram below shows a doubly linked list of characters that could be used to represent the string "ran".

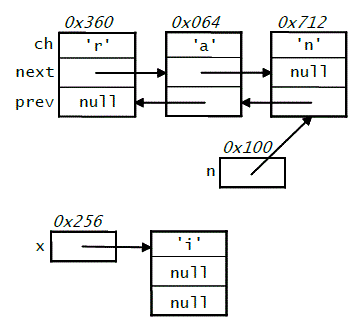
Each of the nodes shown is an instance of the following class:

public class DNode {
    private char ch;
    private DNode next;
    private DNode prev;
}

(In the diagram, we have labeled the individual fields of the DNode object that contains the character 'r'.)

In addition to the list representing "ran", the diagram shows an extra node containing the character 'i', and two reference variables: n, which holds a reference to the third node in the list (the 'n' node); and x, which holds a reference to the 'i' node. The diagram also shows memory addresses of the start of the variables and objects. For example, the 'r' node begins at address 0x360.

1. (6 points) Complete the table that we have provided in ps6_partI, filling in the address and value of each expression from the left-hand column. You should assume the following:

   • the address of the ch field of a DNode is the same as the address of the DNode itself

   • the address of the next field of a DNode is 2 more than the address of the DNode itself

   • the address of the prev field of a DNode is 6 more than the address of the DNode itself, which means that it is also 4 more than the address of the next field.

2. (3 points) Write a Java code fragment that inserts the 'i' node between the 'a' node and the 'n' node, producing a linked list that represents the string "rain". Your code fragment should consist of a series of assignment statements. You should not make any method calls, and you should not use any variables other than the ones provided in the diagram. You may assume that your code is part of the main method in the DNode class, and thus it has direct access to the private fields of the DNode objects.

   Make sure that the resulting doubly linked list has correct values for the next and prev fields in all nodes.

Submitting your work for Part I

Note: There are separate instructions at the end of Part II that you should use when submitting your work for that part of the assignment.

Submit your ps6_partI.pdf file using these steps:

1. If you still need to create a PDF file, open your ps6_partI file on Google Drive, choose File->Download->PDF document, and save the PDF file on your machine.

2. Login to Gradescope by clicking the link in the left-hand navigation bar, and click on the box for CS 112.

3. Click on the name of the assignment (PS 5: Part I) in the list of assignments on Gradescope. You should see a pop-up window labeled Submit Assignment. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

4. Choose the Submit PDF option, and then click the Select PDF button and find the PDF file that you created. Then click the Upload PDF button.

5. You should see a question outline along with thumbnails of the pages from your uploaded PDF. For each question in the outline:

   • Click the title of the question.
   • Click the page(s) on which your work for that question can be found.

   As you do so, click on the magnifying glass icon for each page and doublecheck that the pages that you see contain the work that you want us to grade.

6. Once you have assigned pages to all of the questions in the question outline, click the Submit button in the lower-right corner of the window. You should see a box saying that your submission was successful.

Part II

50 points total

Getting started

1. If you haven’t already done so, create a folder named ps6 for your work on this assignment. You can find instructions for doing so here.

2. Download our Sort class, making sure to save it in your ps6 folder.

3. In VS Code, select the File->Open Folder or File->Open menu option, and use the resulting dialog box to find and open your ps6 folder. (Note: You must open the folder; it is not sufficient to simply open the file.)

Problem 7: Finding the union of two arrays

20 points total; individual-only

In a file named MergeApproach.java, implement a static method named union that takes two arrays of integers as parameters and uses an approach based on merging to find and return the intersection of the two arrays – i.e., all values that are found in both arrays.

The method should have the following header

public static int[] union(int[] a1, int[] a2)

It should take two arrays of integers a1 and a2, and it should use an approach based on merging to create and return a new array containing the union of the values in a1 and a2 – i.e., all values that are found in one or both of the original arrays. The result should be in sorted order, and it should not include any duplicate values. For example, the following test code:

int[] a1 = {10, 5, 7, 5, 9, 4};
int[] a2 = {7, 5, 15, 7, 7, 9, 10};
int[] result1 = union(a1, a2);
System.out.println("result1: " + Arrays.toString(result1));

int[] a3 = {0, 2, -4, 6, 10, 8};
int[] a4 = {12, 0, -4, 8};
int[] result2 = union(a3, a4);
System.out.println("result2: " + Arrays.toString(result2));

should display:

result1: [4, 5, 7, 9, 10, 15, 0, 0, 0, 0, 0, 0, 0]
result2: [-4, 0, 2, 6, 8, 10, 12, 0, 0, 0]

(Note that we end up with extra 0s at the end of both of these result arrays for reasons that are discussed below.)

For full credit, your method must be as efficient as possible. See below for more details.

Required approach

1. Begin by creating a new array for the union, giving it a length that is the sum of the lengths of the two original arrays.

2. Use one of the more efficient sorting algorithms from our Sort class to sort both of the original arrays. If you have downloaded our Sort class into the same folder as your Problem5 class (see the Getting started section above), you should be able to make method calls to an appropriate method in the Sort class from within your union method.

3. Find the union of the two arrays by employing an approach that is similar to the one that we used to merge two sorted subarrays (i.e., the approach taken by the merge method in Sort.java)—using indices to “walk down” the two original arrays and copy their values into the array that you created for the union.

   Important notes:

   • One important difference between merging and finding the union is that the union should not include any duplicates. In other words, a given number that appears in one or both of the original arrays should appear exactly once in the union. As a result, you will need to include code that skips over duplicate values as needed as you walk down the original arrays.

   • Your algorithm should be as efficient as possible. In particular, you should perform at most one complete pass through each of the arrays.

4. At the end of the method, return a reference to the array containing the union.

5. Add test code for your method to a main method. Recall that that you can use the Arrays.toString() method to convert an array to a string; import the java.util. package to gain access to the Arrays class. In addition to the cases shown above, you should include at least one other test case that you create.

Notes:

• Because we don’t include duplicates in the result, the number of values in the union (call it x) can be smaller than the length of the results array (which should be the sum of the lengths of the original arrays). In such cases, you should end up with extra 0s at the end of the results array as shown in both of our test cases above.

  If 0 appears in one or both of the original arrays, it will also show up earlier in the results array as part of the union, as it does in our second example above.

• If either a1 or a2 is null, the method should throw an `IllegalArgumentException.

Problem 8: Finding pairs that sum to k

15 points; pair-optional

This is the only problem of the assignment that you may complete with a partner. See the rules for working with a partner on pair-optional problems for details about how this type of collaboration must be structured.

Suppose you are given an array of n integers, and you need to find all pairs of values in the array (if any) that sum to a given integer k. In a class named PairFinder, write code that performs this task for you and outputs all of the pairs that it finds. For example, if k is 12 and the array is initialized as: {10, 4, 7, 7, 8, 5, 15}, your code should output something like the following:

4 + 8 = 12
7 + 5 = 12
7 + 5 = 12

Note that we get two 7 + 5 sums because 7 appears twice in the array. However, while the methods that you write may print a given pair of values more than once in such cases, it is not necessary to do so. In addition, the order in which the sums (and the terms within each sum) are printed does not matter. If no pairs are found, the methods do not need to print anything.

In a file named PairFinder.java, implement the following:

1. A static method named findPairSums() that requires O(n²) steps to solve this problem. The method should have the following header:

   public static void findPairSums(int k, int[] arr)
   

   In addition, you should add test code for it to a main method. You may find it helpful to call the randomArray() method from our SortCount class to generate test arrays, although it also makes sense to use literal arrays that you define.

2. Implement a static method named findPairSumsFaster() that takes the same parameters as findPairSums, but that requires only O(nlogn) steps in the average case to solve this problem. (Hint: you should begin by sorting the array using one of the methods from our Sort class. Once you have done so, only O(n) additional steps are needed to find the pairs.) Here again, you should add test code to the main method.

Problem 9: A merge-like approach to finding the intersection of two arrays

15 points; individual-only

In the file MergeApproach.java you created for Problem #7, implement another static method named intersect that takes two arrays of integers as parameters and uses an approach based on merging to find and return the intersection of the two arrays – i.e., all values that are found in both arrays.

More specifically, you should do the following:

1. Begin by creating a new array for the intersection. What should the length of this array be?

2. Use one of the more efficient sorting algorithms from Sort.java to sort both of the arrays.

3. Find the intersection of the two arrays by employing an approach that is similar to the one that we used to merge two sorted subarrays (i.e., the approach taken by the merge method in Sort.java). Your method should not actually merge the two arrays, but it should take a similar approach—using indices to “walk down” the two arrays, and making use of the fact that the arrays are sorted. As the elements of the intersection are found, put them in the array that you created at the start of the method.

   For full credit:

   • The intersection that you create should not have any duplicates.

   • Your algorithm should be as efficient as possible. In particular, you should perform at most one complete pass through each of the arrays.

4. At the end of the method, return a reference to the array containing the intersection.

5. Add test code for your method to the main method. Recall that that you can use the Arrays.toString() method to convert an array to a string; import the java.util. package to gain access to the Arrays class.

Example #1:

int[] a1 = {10, 5, 7, 5, 9, 4};
int[] a2 = {7, 5, 15, 7, 7, 9, 10};
int[] result = intersect(a1, a2);
System.out.println( result );

You should expect to see:

[5, 7, 9, 10, 0, 0]

Example #2:

int[] a1 = {0, 2, -4, 6, 10, 8};
int[] a2 = {12, 0, -4, 8};
int[] result = intersect(a1, a2);
System.out.println( result );

You should expect to see:

[-4, 0, 8, 0]

Notes:

• The array containing the intersection has the same length as the shorter of the original arrays.

• When the number of values in the intersection (call it n) is smaller than the length of the shorter array, we end up with extra 0s at the end of the array containing the intersection. This happens because the array of integers that we create is initially filled with 0s, and we only use the first n positions of the array.

Problem 10: Rewriting linked-list methods

50 points; individual-only

In lecture, we’ve been looking at linked lists of characters that are composed of objects from the StringNode class. The class includes a variety of methods for manipulating these linked lists, and many of these methods provide functionality that is comparable to the methods found in Java String objects.

Some of the existing StringNode methods use recursion, while others use iteration (i.e., a loop!). In this problem, you will rewrite several of the methods so that they use the alternative approach.

0. Begin by downloading the StringNode class, storing it in your ps7 folder.

   In VS Code, select the File->Open Folder or File->Open menu option, and use the resulting dialog box to find and open your ps7 folder. (Note: You must open the folder; it is not sufficient to simply open the file.)

   The name of the folder should appear in the Explorer pane on the left-hand side of the VS Code window, along with the name of the downloaded file. Click on the name of the file to open an editor window for it.

1. Rewrite the length() method. Remove the existing recursive implementation of the method, and replace it with one that uses iteration instead.

2. Rewrite the toUpperCase() method. Remove the existing iterative implementation of the method, and replace it with one that uses recursion instead. No loops are allowed.

3. Rewrite the printReverse() method so that it uses iteration. This method is easy to implement using recursion–as we have done in StringNode.java–but it’s more difficult to implement using iteration. Here are two possible iterative approaches, either of which will receive full credit:

   • reverse the linked list before printing it: This approach is the trickier of the two, but we recommend it because it uses less memory, and it will give you more practice with manipulating linked lists. Remember that you may not use the toString() method for this or any other method. In addition, you should not use the print() method. Finally, don’t forget to restore the linked list to its original form!

   • use an array: Create an array of type char that is large enough to hold all of the characters in the string and use it to help you with the problem.

4. Rewrite the removeFirst() method. Remove the existing iterative implementation of the method, and replace it with one that uses recursion instead. No loops are allowed.

5. Rewrite the copy() method. Remove the existing recursive implementation of the method, and replace it with one that uses iteration instead.

6. Rewrite the insertSorted() method. Remove the existing iterative implementation of the method, and replace it with one that uses recursion instead. No loops are allowed.

7. Test your methods thoroughly.

   • There is existing test code in the main() method. Leave that code intact, and use it to test your new versions of the methods.

   • You are also strongly encouraged to add other tests to this method, although doing so is not strictly required.

   • As mentioned in the guidelines at the start of the problem, the provided toString() method means that you can print a StringNode s in order to see the portion of the linked-list string that begins with s.

   • Another useful method for testing is the convert() method, which converts a Java String object into the corresponding linked-list string.

   • You may also find it helpful to download the following file into your ps7 folder: StringNodeOrig.java.

     It contains the original version of the StringNode class, so that you can compare the behavior of the original methods to the behavior of your revised methods.

Submitting your work for Part II

Note: There are separate instructions at the end of Part I that you should use when submitting your work for that part of the assignment.

You should submit only the following files for the PS6 submission portal:

• MergeApproach.java
• PairFinder.java

You should submit the following file under the special STRINGNODE submission portal:

• StringNode.java

Make sure that you do not try to submit a .class file or a file with a ~ character at the end of its name.

Here are the steps:

1. Login to Gradescope as needed by clicking the link in the left-hand navigation bar, and then click on the box for CS 112.

2. Click on the name of the assignment (PS 6: Part II) in the list of assignments. You should see a pop-up window with a box labeled DRAG & DROP. (If you don’t see it, click the Submit or Resubmit button at the bottom of the page.)

3. Add your files to the box labeled DRAG & DROP. You can either drag and drop the files from their folder into the box, or you can click on the box itself and browse for the files.

4. Click the Upload button.

5. You should see a box saying that your submission was successful. Click the (x) button to close that box.

6. The Autograder will perform some tests on your files. Once it is done, check the results to ensure that the tests were passed. If one or more of the tests did not pass, the name of that test will be in red, and there should be a message describing the failure. Based on those messages, make any necessary changes. Feel free to ask a staff member for help.

   Note: You will not see a complete Autograder score when you submit. That is because additional tests for at least some of the problems will be run later, after the final deadline for the submission has passed. For such problems, it is important to realize that passing all of the initial tests does not necessarily mean that you will ultimately get full credit on the problem. You should always run your own tests to convince yourself that the logic of your solutions is correct.

7. If needed, use the Resubmit button at the bottom of the page to resubmit your work. Important: Every time that you make a submission, you should submit all of the files for that Gradescope assignment, even if some of them have not changed since your last submission.

8. Near the top of the page, click on the box labeled Code. Then click on the name of each file to view its contents. Check to make sure that the files contain the code that you want us to grade.