Final Project

150 points; pair-optional

• Parts I and II should be submitted as part of Problem Set 10 by 11:59 p.m. on Sunday, April 22, 2018

• The full project is due by 11:59 p.m. on Tuesday, May 1, 2018

Important: This assignment cannot be replaced by the final exam, so it is essential that you complete it.

Preliminaries

For the remainder of the semester, you will be working on a final course project. The project is a bit larger in scope than a problem set and is thus worth 150 points. We encourage you to read through the final project description in its entirety before starting.

You may work on the project individually or as a pair. Since this is a large project, we especially encourage you to work in pairs, but please review the collaboration policies of the course before doing so.

If you have questions while working on the final project, please come to office hours, post them on Piazza, or email cs111-staff@cs.bu.edu.

Make sure to submit your work on Apollo, following the procedures found at the end of the instructions.

Project Overview

As discussed in lecture, many problems can be framed as a search for a series of actions that take you from some initial state to some goal state. Examples include robot navigation, route finding, and map labeling. For such a problem, the state space of the problem is the collection of all states that can be reached by starting in the initial state and applying some number of actions. State-space search is the technical term given to the process of searching through the state space for a path to the goal state, and many different algorithms have been developed for that process.

The project involves applying state-space search to a classic problem known as the Eight Puzzle, which we’ve discussed in lecture. The Eight Puzzle is a 3x3 grid containing 8 numbered tiles and one empty or blank cell. Here is one possible configuration of the tiles, with the blank cell shown shaded blue:

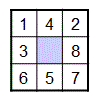
Tiles that are adjacent to the blank cell can move into that position in the grid, and solving the puzzle involves moving the tiles until you reach the following goal state:

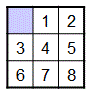
In this project, you will apply state-space search to solve any valid initial configuration of the Eight Puzzle.

Some parts of the project will be required – including an implementation of several classic state-space algorithms – but other parts will be left to your creativity. In particular, you will see that some initial configurations of the Eight Puzzle – ones that require a large number of moves – can be difficult to solve in a reasonable amount of time, and you will be encouraged to develop variations on the required algorithms that will reduce the time needed to find a solution!

Project Description

Part I: A Board class for the Eight Puzzle

For the first part of the project, you will create an initial version of a Board class for objects that represent an Eight Puzzle board.

Your tasks

0. Begin by downloading the following zip file: project.zip

   Unzip this archive, and you should find a folder named project, and within it a number of files, including board.py. Open that file in IDLE, and put your work for this part of the project in that file. You should not move any of the files out of the project folder.

1. We have given you the start of a constructor __init__(self, digitstr) that accepts a string input digitstr and assigns preliminary values to the following three attributes:

   • tiles: a reference to a 2-D list of integers with 3 rows and 3 columns that will be used to store the contents of the board. Initially, this 2-D list is filled with zeros.

   • blank_r: an integer representing the row of the blank cell; this is initially set to -1

   • blank_c: an integer representing the column of the blank cell; this is also initially set to -1

   The input digitstr is a 9-character string of digits that specifies the desired configuration of the tiles. For example, consider the following puzzle: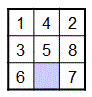

   

   It would be represented by the string '142358607'. Notice that:

   • the first 3 characters in the string (142) specify the contents of the first row
   • the next 3 characters (358) specify the contents of the second row
   • the final 3 characters (607) specify the contents of the last row, with 0 representing the blank cell.

   Leaving our starter code alone, add code below it that updates the values of the three Board attributes to reflect the input digitstr. For the string '142358607' described above, you should end up with the following values:

   • tiles should be [[1, 4, 2], [3, 5, 8], [6, 0, 7]]
   • blank_r should be 2, since the blank cell is in row 2
   • blank_c should be 1, since the blank cell is in column 1

   There are multiple options for processing the input digitstr, but you should use at least one loop. Here are some hints:

   • The tile at row r, column c gets its value from the digit at position (3*r + c) of the input string digitstr. For example, the tile at row 1, column 2 in the above puzzle is an 8, and that corresponds to digitstr[3*1 + 2] (i.e., position 5 in the string '142358607').

   • You can use the int() function to convert the string version of a digit to the appropriate integer.

   • Don’t forget to record the row and column numbers of the blank cell in the attributes blank_r and blank_c.

   Examples:

   >>> b = Board('142358607')
   >>> b.tiles
   [[1, 4, 2], [3, 5, 8], [6, 0, 7]]
   >>> b.blank_r
   2
   >>> b.blank_c
   1
   >>> b2 = Board('631074852')
   >>> b2.tiles
   [[6, 3, 1], [0, 7, 4], [8, 5, 2]]
   >>> b2.blank_r
   1
   >>> b2.blank_c
   0
   

2. Write a method __repr__(self) that returns a string representation of a Board object.

   In the string that __repr__ constructs, each numeric tile should be represented by the appropriate single-character string, followed by a single space. The blank cell should be represented by an underscore character ('_') followed by a space; make sure that you do not accidentally use a hyphen ('-'). There should be a newline character ('\n') after the characters for each row, so that each row will appear on a separate line when you evaluate or print a Board object. For example:

   >>> b = Board('142358607')
   >>> b
   1 4 2 
   3 5 8 
   6 _ 7
   
   >>> str(b)
   '1 4 2 \n3 5 8 \n6 _ 7 \n'
   

   Note that calling str(b) from the Shell allows us to see the full string returned by __repr__, including all of the spaces and newline characters. Make sure that your results for this call match ours.

   Hints:

   • This __repr__ will be similar to the one that you wrote for the Board class in Problem Set 9. You may want to use that method as a model, and to consult the hints that we gave you for that problem.

   • Remember that the __repr__ method needs to return a string, and that it should not do any printing.

   • You can use the str() function to convert an integer to a string.

   • Make sure that your __repr__ doesn’t change the object in any way. In particular, the tiles list should not change:

     >>> b = Board('142358607')
     >>> b.tiles
     [[1, 4, 2], [3, 5, 8], [6, 0, 7]]
     >>> b
     1 4 2 
     3 5 8 
     6 _ 7
     
     >>> b.tiles
     [[1, 4, 2], [3, 5, 8], [6, 0, 7]]
     

3. As discussed in lecture, we can simplify things by imagining that all Eight-Puzzle moves involve “moving” the blank cell. For example, in the puzzle below

   

   moving the blank up is equivalent to moving the 5 down, which produces the following board:

   

   Write a method move_blank(self, direction) that takes as input a string direction that specifies the direction in which the blank should move, and that attempts to modify the contents of the called Board object accordingly. Not all moves are possible on a given Board; for example, it isn’t possible to move the blank down if it is already in the bottom row. The method should return True or False to indicate whether the requested move was possible.

   Notes/hints:

   • The input direction can have one of the following four values: 'up', 'down', 'left', 'right'. If any other value is passed in for ‘direction’, the method should print an error message and return False without making any changes to the object.

   • Here is one possible approach to this method:

     • Start by determining the new row and column coordinates of the blank cell, based on the value of direction. At first, you should store these new coordinates in temporary local variables, not in the attributes themselves.

     • Check to see if either of the new coordinates would take you off of the board. If so, simply return False.

     • Otherwise, make the necessary changes to the Board object’s attributes and return True. Draw some pictures to help you figure out the appropriate changes. We recommend changing the necessary elements of self.tiles before changing self.blank_r or self.blank_c.

   Examples:

   >>> b = Board('142358607')
   >>> b
   1 4 2 
   3 5 8 
   6 _ 7
   
   >>> b.move_blank('up')
   True
   >>> b
   1 4 2 
   3 _ 8 
   6 5 7
   
   >>> b.tiles      # tiles should still contain only integers
   [[1, 4, 2], [3, 0, 8], [6, 5, 7]]
   >>> b.blank_r
   1
   >>> b.blank_c
   1  
   >>> b.move_blank('left')
   True
   >>> b
   1 4 2 
   _ 3 8 
   6 5 7
   
   >>> b.blank_r
   1
   >>> b.blank_c
   0  
   >>> b.move_blank('left')   # can't go any further left
   False
   >>> b                      # b is unchanged
   1 4 2 
   _ 3 8 
   6 5 7
   
   >>> b.move_blank('down')
   True
   >>> b
   1 4 2 
   6 3 8 
   _ 5 7
   
   >>> b.move_blank('right')
   True
   >>> b
   1 4 2 
   6 3 8 
   5 _ 7
   
   >>> b.move_blank('RIGHT')
   unknown direction: RIGHT
   False
   >>> b                      # b is unchanged
   1 4 2 
   6 3 8 
   5 _ 7
   
   >>> b.blank_r
   2
   >>> b.blank_c
   1
   

4. Write a method digit_string(self) that creates and returns a string of digits that corresponds to the current contents of the called Board object’s tiles attribute. For example:

   >>> b = Board('142358607')
   >>> b.digit_string()
   '142358607'
   

   Note that this call to digit_string() returns the string of digits that was used when creating the Board. However, this won’t always be the case, because the string returned by digit_string() should reflect any changes that have been made to the tiles. For example, consider this continuation of the above example:

   >>> b.move_blank('right')
   True
   >>> b.move_blank('up')
   True
   >>> b.digit_string()
   '142350678'
   

5. Write a method copy(self) that returns a newly-constructed Board object that is a deep copy of the called object (i.e., of the object represented by self).

   This method should use the Board constructor to create a new Board object with the same configuration of tiles as self, and it should return the newly created Board object.

   Hint: The Board constructor takes a string of digits. How could you easily obtain the appropriate string of digits for the called Board?

   Examples:

   >>> b = Board('142358607')
   >>> b
   1 4 2 
   3 5 8 
   6 _ 7
   
   >>> b2 = b.copy()
   >>> b2
   1 4 2 
   3 5 8 
   6 _ 7
   
   >>> b2.move_blank('up')
   True
   >>> b2
   1 4 2 
   3 _ 8 
   6 5 7
   
   >>> b    # the original Board is unchanged
   1 4 2 
   3 5 8 
   6 _ 7
   

6. Write a method num_misplaced(self) that counts and returns the number of tiles in the called Board object that are not where they should be in the goal state. You should not include the blank cell in this count, even if it’s not where it should be in the goal state. For example:

   >>> b = Board('142358607')
   >>> b
   1 4 2 
   3 5 8 
   6 _ 7 
   >>> b.num_misplaced()       # 1,4,5,7,8 tiles are out of place
   5
   >>> b.move_blank('right')   # move 7 tile where it belongs
   True
   >>> b   
   1 4 2 
   3 5 8 
   6 7 _ 
   >>> b.num_misplaced()       # 1,4,5,8 tiles are still out of place
   4
   

7. Finally, write a method __eq__(self, other) that overloads the == operator – creating a version of the operator that works for Board objects. The method should return True if the called object (self) and the argument (other) have the same values for the tiles attribute, and False otherwise.

   This method should be straightforward to implement because you can simply use the == operator to compare self.tiles and other.tiles. You do not need to explicitly compare the individual tiles yourself, because the == operator already compares the individual elements of 2-D lists.

   Examples:

   >>> b1 = Board('012345678')
   >>> b2 = Board('012345678')
   >>> b1 == b2
   True
   >>> b2.move_blank('right')
   True
   >>> b1 == b2
   False
   

Part II: A State class

For the second part of the project, you will create a preliminary State class for objects that represent one of the states in a state-space search tree for the Eight Puzzle. We discussed State objects and their connection to the search tree in lecture.

Your tasks

0. Find the file state.py in your project folder and open it in IDLE. It contains starter code for the State class. Read over the comments accompanying the starter code.

1. Write a constructor __init__(self, board, predecessor, move) that constructs a new State object by initializing the following four attributes:

   • an attribute board that stores a reference to the Board object associated with this state, as specified by the parameter board

   • an attribute predecessor that stores a reference to the State object that comes before this state in the current sequence of moves, as specified by the parameter predecessor

   • an attribute move that stores a string representing the move that was needed to transition from the predecessor state to this state, as specified by the parameter move

   • an attribute num_moves that stores an integer representing the number of moves that were needed to get from the initial state (the state at the root of the tree) to this state. If predecessor is None–which means that this new state is the initial state–then num_moves should be initialized to 0. Otherwise, it should be assigned a value that is one more that the number of moves for the predecessor state.

   Because we’ve already given you an __repr__ method for the class, you should be able to test your constructor as follows:

   >>> b1 = Board('142358607')
   >>> s1 = State(b1, None, 'init')
   >>> s1
   142358607-init-0
   >>> b2 = b1.copy()
   >>> b2.move_blank('up')
   True
   >>> s2 = State(b2, s1, 'up')    # s1 is the predecessor of s2
   >>> s2
   142308657-up-1
   

2. Write a method is_goal(self) that returns True if the called State object is a goal state, and False otherwise.

   At the top of the file, we’ve given you a 2-D list called GOAL_TILES that represents the configuration of the tiles in a goal state. You can simply use the == operator to compare the tiles attribute in the Board object associated with this state to GOAL_TILES.

   Here are some test cases:

   >>> s1 = State(Board('102345678'), None, 'init')
   >>> s1.is_goal()
   False
   >>> s2 = State(Board('012345678'), s1, 'left')
   >>> s2.is_goal()
   True
   

3. Write a method generate_successors(self) that creates and returns a list of State objects for all successor states of the called State object. We discussed the concept of successor states in lecture.

   At the top of the file, we’ve given you a list called MOVES that contains the names of the four possible ways in which the blank cell can be moved:

   MOVES = ['up', 'down', 'left', 'right']
   

   For each of these moves, the method should do the following:

   • Create a copy of the Board object associated with this state by using the appropriate method in that Board object.

   • Attempt to apply the move by using the appropriate method in the new Board object (i.e., the copy). Make sure that you apply the move to the copy, and not to the original.

   • If the move was successful, construct a new State object for the new Board, and add that State object to the list of successors. Otherwise, don’t create a State object for that move.

   Then, once you are done trying all possible moves, return the list of successors. Here’s some pseudocode for the full method:

   def generate_successors(self):
       successors = []
       for each move m in the list MOVES:
           b = a copy of self.board
           try applying the move m to b
           if you can apply it:
               construct a new State object for the result of the move
               add the new State object to successors
       return successors
   

   Hints:

   • Make sure to take advantage of the appropriate methods in the Board objects.

   • When constructing a new State object, you should use the variable self as the second input of the constructor, since the current state (the one represented by the called object) is the predecessor of the new state.

   Examples:

   >>> b1 = Board('142358607')
   >>> b1
   1 4 2 
   3 5 8 
   6 _ 7
   
   >>> s1 = State(b1, None, 'init')
   >>> s1
   142358607-init-0
   >>> succ = s1.generate_successors()   
   >>> succ            # 3 successors; blank can't go down from bottom row
   [142308657-up-1, 142358067-left-1, 142358670-right-1]
   >>> s1              # s1 should be unchanged
   142358607-init-0
   >>> succ[2]                        # in succ[2], blank is in lower-right
   142358670-right-1
   >>> succ[2].generate_successors()  # blank can go up or left
   [142350678-up-2, 142358607-left-2]
   >>> succ[0]                        # in succ[0], blank is in middle
   142308657-up-1
   >>> succ[0].generate_successors()  # blank can go in all four directions
   [102348657-up-2, 142358607-down-2, 142038657-left-2, 142380657-right-2]
   

Part III: A Searcher class for random search

In the next part of the project, you will begin to implement the actual state-space search process. As discussed in lecture, we will use searcher objects to perform the search for us. Different types of searcher objects will implement different state-space search algorithms, and we’ll take advantage of inheritance when defining the searcher classes.

0. Find the file searcher.py in your project folder and open it in IDLE. It contains some starter code, including the beginnings of a class called Searcher, which will perform a random state-space search. Read over the comments accompanying the starter code.

1. Write a constructor __init__(self, depth_limit) that constructs a new Searcher object by initializing the following attributes:

   • an attribute states for the Searcher‘s list of untested states; it should be initialized to an empty list

   • an attribute num_tested that will keep track of how many states the Searcher tests; it should be initialized to 0

   • an attribute depth_limit that specifies how deep in the state-space search tree the Searcher will go; it should be initialized to the value specified by the parameter depth_limit.
     (A depth_limit of -1 will be used to indicate that the Searcher does not use a depth limit.)

   Because we’ve already given you an __repr__ method for the class, you should be able to test your constructor as follows:

   >>> searcher1 = Searcher(-1)    # -1 means no depth limit
   >>> searcher1
   Searcher: 0 untested, 0 tested, no depth limit
   >>> searcher2 = Searcher(10)
   >>> searcher2
   Searcher: 0 untested, 0 tested, depth limit = 10
   

2. Write a method add_state(self, new_state) that adds takes a single State object called new_state and adds it to the Searcher‘s list of untested states. This method should only require one line of code! It should not return a value.

   For the sake of efficiency, we recommend that you do not do something like the following:

   self.states = self.states + ...     # don't do this!
   

   Rather, we recommend that you either use the += operator or the append method in the list object. We will discuss the reasons for this in lecture.

   Examples:

   >>> searcher = Searcher(-1)
   >>> searcher.states
   []
   >>> s = State(Board('142358607'), None, 'init')
   >>> searcher.add_state(s)
   >>> searcher.states
   [142358607-init-0]
   >>> succ = s.generate_successors()
   >>> succ
   [142308657-up-1, 142358067-left-1, 142358670-right-1]
   >>> searcher.add_state(succ[0])  # add just the first successor
   >>> searcher.states
   [142358607-init-0, 142308657-up-1]
   

3. Write a method should_add(self, state) that takes a State object called state and returns True if the called Searcher should add state to its list of untested states, and False otherwise.

   The method should return False if either of these conditions holds:

   • the Searcher has a depth limit (i.e., its depth limit is not -1) and state is beyond the depth limit (i.e., the number of moves used to get to state is greater than the depth limit)

   • state creates a cycle in the search, because the same board already appears in the sequence of moves that led to state. We’ve given you a method in the State class called creates_cycle() that checks for this. Read the comments accompanying that method to understand how it works, and apply it appropriately here.

   If neither of these conditions holds, the method should return True.

   Examples:

   >>> searcher = Searcher(-1)       # no depth limit
   >>> b1 = Board('142358607')
   >>> s1 = State(b1, None, 'init')  # initial state
   >>> searcher.add_state(s1)
   >>> b2 = b1.copy()
   >>> b2.move_blank('left')
   True
   >>> s2 = State(b2, s1, 'left')    # s2's predecessor is s1
   >>> searcher.should_add(s2)
   True
   >>> b3 = b2.copy()
   >>> b3.move_blank('right')        # get the same board as b1 
   True
   >>> s3 = State(b3, s2, 'right')   # s3's predecessor is s2
   >>> searcher.should_add(s3)       # adding s3 would create a cycle
   False
   >>> b3.move_blank('left')         # reconfigure b3
   True
   >>> b3.move_blank('up')
   True
   >>> s3 = State(b3, s2, 'up')      # recreate s3 with new b3 (no cycle)
   >>> s3.num_moves
   2
   >>> searcher.should_add(s3)       # no depth limit and no cycle
   True
   >>> searcher.depth_limit = 1      # change depth limit to 1 move!
   >>> searcher.should_add(s3)       # s3 is now beyond the depth limit
   False
   

4. Write a method add_states(self, new_states) that takes a list State objects called new_states, and that processes the elements of new_states one at a time as follows:

   • If a given state s should be added to the Searcher‘s list of untested states (because s would not cause a cycle and is not beyond the Searcher‘s depth limit), the method should use the Searcher‘s add_state() method to add s to the list of states.

   • If a given state s should not be added to the Searcher object’s list of states, the method should ignore the state.

   This method should not return a value.

   Notes/hints:

   • Take advantage of the Searcher‘s method for determining if a state should be added.

   • Make sure that you use add_state() when adding the individual states to the list, rather than adding them yourself. This will will allow you to make fewer changes when you use inheritance to define other types of searchers.

   Examples:

   >>> searcher = Searcher(-1)
   >>> s = State(Board('142358607'), None, 'init')
   >>> searcher.add_state(s)       # note: add_state, not add_states!
   >>> searcher.states
   [142358607-init-0]
   >>> succ = s.generate_successors()
   >>> succ
   [142308657-up-1, 142358067-left-1, 142358670-right-1]
   >>> searcher.add_states(succ)   # add_states, not add_state
   >>> searcher.states
   [142358607-init-0, 142308657-up-1, 142358067-left-1, 142358670-right-1]
   >>> succ[-1]
   142358670-right-1
   >>> succ2 = succ[-1].generate_successors() 
   >>> succ2
   [142350678-up-2, 142358607-left-2]
   >>> searcher.add_states(succ2)
   >>> searcher.states
   [142358607-init-0, 142308657-up-1, 142358067-left-1, 142358670-right-1, 142350678-up-2]
   

   Note that the last call to add_states above took a list of two states (the list given by succ2), but that only one of them (the state 142350678-up-2) was actually added to searcher‘s list of states. That’s because the other state (142358607-left-2) has the same board as the initial state and would thus create a cycle.

5. Copy the following method into your Searcher class:

   def next_state(self):
       """ chooses the next state to be tested from the list of 
           untested states, removing it from the list and returning it
       """
       s = random.choice(self.states)
       self.states.remove(s)
       return s
   

   Make sure to maintain the appropriate indentation when you do so.

   This method will be used to obtain the next state to be tested, and you should review it carefully. Here are two points worth noting:

   • Because Searcher objects perform a random search through the search space, we are using the random.choice method to randomly choose one of the elements of the states list.

   • We’re using a list method called remove to remove the selected state s from the states list.

6. Finally, write a method find_solution(self, init_state) that performs a full state-space search that begins at the specified initial state init_state and ends when the goal state is found or when the Searcher runs out of untested states.

   • The searcher should begin by adding init_state to its list of states. Make sure to use the existing add_state() method to do so.

   • If the searcher finds a goal state, it should return it.

   • If the searcher runs out of untested states before finding a goal state, it should return the special keyword None. (Note that there should not be any quotes around None, because it is not a string.)

   • The method should increment the Searcher object’s num_tested attribute every time that it tests a state to see if it is the goal.

   We will give you pseudocode for this method in lecture.

   Make sure that you take advantage of existing methods – both those available in the Searcher (i.e., in self) and those available in the State objects. Among other methods, you should use the Searcher object’s next_state() method to obtain the next state to be tested.

   Example 1:

   >>> searcher = Searcher(-1)
   >>> s = State(Board('012345678'), None, 'init')   # init is a goal state!
   >>> s
   012345678-init-0
   >>> searcher.find_solution(s)    # returns init state, because it's a goal state
   012345678-init-0
   >>> searcher
   Searcher: 0 untested, 1 tested, no depth limit
   

   Example 2 (results will vary because of randomness):

   >>> searcher = Searcher(-1)
   >>> searcher
   Searcher: 0 untested, 0 tested, no depth limit
   >>> s = State(Board('142358607'), None, 'init')   
   >>> searcher.find_solution(s)    # returns goal state at depth 5
   012345678-left-5
   >>> searcher
   Searcher: 22 untested, 28 tested, no depth limit
   >>> searcher = Searcher(-1)      # a new searcher, also with no depth limit
   >>> searcher
   Searcher: 0 untested, 0 tested, no depth limit
   >>> searcher.find_solution(s)    # returns goal state at depth 13
   012345678-left-13
   >>> searcher
   Searcher: 768 untested, 1041 tested, no depth limit
   

7. In order to see the full solution (i.e., the sequence of moves from the initial state to the goal state), we need to add a method to the State class that will follow predecessor references back up the state-space search tree in order to find and print the sequence of moves.

   Open up your state.py file, and add a method print_moves_to(self) that prints the sequence of moves that lead from the initial state to the called State object (i.e., to self).

   To accomplish this task, you should first review the attributes that each State object has inside it. Consult the guidelines for the State class __init__ method as needed.

   Next, it’s worth noting that this method will be starting at a given State object and following predecessor references back to the initial state. However, we want to print the sequence of moves in the reverse order – from the initial state to the called State object. One way to do this is using recursion, as shown in the following pseudocode:

   def print_moves_to(self):
       if self is the initial state:    # base case
           print('initial state:')
           print the board associated with self
       else:
           make a recursive call to print the moves to the predecessor state
           print the move that led to self (see format below)
           print the board associated with self
   

   Because the recursive call on the predecessor state comes before the processing of self, the method will print the sequence of moves in the correct order.

   Example (results will vary because of randomness):

   >>> b = Board('142305678')    # only 2 moves from a goal
   >>> b
   1 4 2 
   3 _ 5 
   6 7 8
   
   >>> s = State(b, None, 'init')   
   >>> searcher = Searcher(-1)
   >>> goal = searcher.find_solution(s)
   >>> goal
   012345678-left-2
   >>> goal.print_moves_to()
   initial state:
   1 4 2 
   3 _ 5 
   6 7 8
   
   move the blank up:
   1 _ 2 
   3 4 5 
   6 7 8
   
   move the blank left:
   _ 1 2 
   3 4 5 
   6 7 8
   
   >>>
   

   Although the sequence of moves may vary because of randomness, the format of the output should be the same as what you see above.

8. Once you have completed all of the methods specified above, you can use the driver function that we have provided to facilitate the process of solving a given puzzle.

   Find the file eight_puzzle.py in your project folder and open it in IDLE. The driver function is called eight_puzzle, and it has two mandatory inputs:

   • a string describing the board configuration for the initial state

   • a string specifying the search algorithm that you want to use; for now, the only option is random.

   • a third input that allows you to specify a parameter for the searcher; for now, it will be used to specify the depth limit.

   Here’s an example of how you would call it:

   >>> eight_puzzle('142358607', 'random', -1)
   

   After finding a solution, the function will ask if you want to see the moves. Enter y to see them, or anything else to end the function without seeing them.

   Important

   After making changes to any of your Python files, you should rerun the eight_puzzle.py file before using the driver function to test your changed code.

Part IV: Subclasses for other search algorithms

In this part of the assignment you will implement other state-space search algorithms by defining classes for new types of searcher objects.

Uninformed state-space search: BFS and DFS

1. In searcher.py, define a class called BFSearcher for searcher objects that perform breadth-first search (BFS) instead of random search. As discussed in lecture, BFS involves always choosing one the untested states that has the smallest depth (i.e., the smallest number of moves from the initial state).

   This class should be a subclass of the Searcher class that you implemented in Part III, and you should take full advantage of inheritance. In particular, you should not need to include any attributes in your BFSearcher class, because all of the necessary attributes will be inherited from Searcher.

   Similarly, you should not need to define many methods, because most of necessary functionality is already provided in the methods that are inherited from Searcher.

   However, you will need to do the following:

   1. Make sure that your class header specifies that BFSearcher inherits from Searcher.

   2. Because all of the attributes of a BFSearcher are inherited from Searcher, you will not need to define a constructor for this class. Rather, we can just use the constructor that is inherited from Searcher.

   3. Write a method next_state(self) that overrides (i.e., replaces) the next_state method that is inherited from Searcher. Rather than choosing at random from the list of untested states, this version of next_state should follow FIFO (first-in first-out) ordering – choosing the state that has been in the list the longest. In lecture, we discussed why this leads to breadth-first search. As with the original version of next_state, this version should remove the chosen state from the list of untested states before returning it.

   Examples:

   >>> bfs = BFSearcher(-1)
   >>> s = State(Board('142358607'), None, 'init')
   >>> s
   142358607-init-0
   >>> bfs.add_state(s)
   >>> succ = s.generate_successors()
   >>> succ
   [142308657-up-1, 142358067-left-1, 142358670-right-1]
   >>> bfs.add_states(succ)
   >>> bfs.next_state()   # should get the initial state
   142358607-init-0
   >>> bfs.next_state()
   142308657-up-1
   >>> bfs.next_state()
   142358067-left-1
   

2. In searcher.py, define a class called DFSearcher for searcher objects that perform depth-first search (DFS) instead of random search. As discussed in lecture, DFS involves always choosing one the untested states that has the largest depth (i.e., the largest number of moves from the initial state).

   DFS, the next state to be tested should be one of the ones that has the largest depth in the state-space search tree.

   Here again, the class should be a subclass of the Searcher class, and you should take full advantage of inheritance. The necessary steps are very similar to the ones that you took for BFSearcher, but the next_state() method should follow LIFO (last-in first-out) ordering – choosing the state that was most recently added to the list.

   Examples:

   >>> dfs = DFSearcher(-1)
   >>> s = State(Board('142358607'), None, 'init')
   >>> dfs.add_state(s)
   >>> succ = s.generate_successors()
   >>> succ
   [142308657-up-1, 142358067-left-1, 142358670-right-1]
   >>> dfs.add_states(succ)
   >>> dfs.next_state()   # the last one added, not the first!
   142358670-right-1
   >>> dfs.next_state()
   142358067-left-1
   

3. In eight_puzzle.py, there is a helper function called create_searcher that is used to create the appropriate type of searcher object. Modify this helper function so that it will be able to create objects that perform BFS and DFS. To do so, simply uncomment the lines that handle cases in which the algorithm input is 'BFS' or 'DFS'. Once you do so, you should be able to use the eight_puzzle driver function to test your BFSearcher and DFSearcher classes.

   Breadth-first search should quickly solve the following puzzle:

   >>> eight_puzzle('142358607', 'BFS', -1)
   BFS: 0.006 seconds, 56 states
   Found a solution requiring 5 moves.
   Show the moves (y/n)?
   

   You may get a different time than we did, but the rest of the results should be the same. As discussed in lecture, BFS finds an optimal solution for eight-puzzle problems, so 5 moves is the fewest possible moves for this particular initial state.

   Depth-first search, on the other hand, ends up going deep in the search tree before it finds a goal state:

   >>> eight_puzzle('142358607', 'DFS', -1)
   DFS: 10.85 seconds, 3100 states.
   Found a solution requiring 3033 moves.
   Show the moves (y/n)?
   

   Important: In cases like this one in which the solution has an extremely large number of moves, trying to show the moves is likely to cause an error. That’s because our print_moves_to method uses recursion, and the number of recursive calls is equal to the number of moves in the solution. Each recursive call adds a new stack frame to the top of the memory stack, and we can end up overflowing the stack when we make that many recursive calls!

   To get a solution from DFS with fewer moves, we can impose a depth limit by passing it a positive integer as the third argument to the eight_puzzle function. For example:

   >>> eight_puzzle('142358607', 'DFS', 25)
   DFS: 6.945 seconds, 52806 states
   Found a solution requiring 23 moves.
   Show the moves (y/n)?
   

   Using a depth limit of 25 keeps DFS from going too far down a bad path, but the resulting solution requires 23 moves, which is still far from optimal!

Informed state-space search: Greedy and A*

4. In searcher.py, complete a class called GreedySearcher for searcher objects that perform greedy search. As discussed in lecture, greedy search is an informed search algorithms that uses a heuristic function to estimate the remaining cost needed to get from a given state to the goal state (for the Eight Puzzle, this is just an estimate of how many additional moves are needed). Greedy Search uses this heuristic function when computing the priority of each state, and it selects the next state based on those priorities.

   To provide an example of what a heuristic function should look like, we’ve given you the following function in searcher.py:

   def h0(state):
       """ a heuristic function that always returns 0 """
       return 0
   

   Note that this is a function, not a method, because it is outside of any class. Note also that it takes a State object as its only parameter, and that it returns an integer. All heuristic functions should have these characteristics.

   Like your BFSearcher and DFSearcher classes, the GreedySearcher class will be a subclass of the Searcher class that you implemented in Part III, and you should take full advantage of inheritance. However, the changes required in this class will be more substantial that the ones in BFSearcher and DFSearcher.

   Among other things, GreedySearcher objects will have a new attribute called heuristic that will allow you to choose among different heuristic functions, and they will also have a new method for computing the priority of a state.

   Here are the necessary steps:

   1. Find the class header that we’ve given you. Note that it specifies that GreedySearcher inherits from Searcher. We have also given you an __repr__ method that overrides the one inherited from Searcher. As a result, you will see somewhat different information when you evaluate or print a GreedySearcher object than you do when you evaluate or print one of the earlier types of searchers.

   2. Write a constructor __init__(self, heuristic) that constructs a new GreedySearcher object.

      The constructor should begin by calling the constructor inherited from the superclass; this will allow that superclass constructor to initialize the inherited attributes. Use the super() function to access the __init__ method in the superclass (as we did in the constructor for the Holiday class from lecture), and pass in a value of -1 to indicate that GreedySearcher objects will not use a depth limit.

      The new constructor should then initialize a new attribute called heuristic, assigning it whatever value is passed in for the heuristic parameter. This attribute will be used to store a reference to the heuristic function used by the searcher.

      Once you have implemented the constructor, you can test it as follows:

      >>> g = GreedySearcher(h0)
      >>> g
      GreedySearcher: 0 untested, 0 tested, heuristic h0
      

      Note that the string produced by the new __repr__ includes the name of the heuristic function used by the searcher.

   3. Copy the following method into the GreedySearcher class:

      def priority(self, state):
          """ computes and returns the priority of the specified state,
              based on the heuristic function used by the searcher
          """
          return -1 * self.heuristic(state)
      

      It computes the priority of the State object passed in as a parameter. Note that it uses the value of self.heuristic to make a function call. This works because self.heuristic is a reference to the heuristic function. In addition, the priority method multiplies the heuristic function’s return value by -1 to ensure that states that the heuristic function thinks are closer to the goal state will end up with higher priorities.

   4. Add a new heuristic function h1(state) that takes a State object called state, and that computes and returns an estimate of how many additional moves are needed to get from state to the goal state. Its estimate should simply be the number of misplaced tiles in the Board object associated with state. Take advantage of the appropriate Board method to determine this value.

      Make sure that h1 is a function, not a method. Use the existing h0 function as a model, and make sure that h1‘s header is not indented.

      Once you have added this function, you can perform the following tests:

      >>> s1 = State(Board('142358607'), None, 'init')
      >>> s2 = State(Board('142358670'), None, 'init')
      >>> h1(s1)    # the board in s1 has 5 misplaced tiles
      5
      >>> h1(s2)    # the board in s2 has 4 misplaced tiles
      4
      >>> g1 = GreedySearcher(h0)   
      >>> g1
      GreedySearcher: 0 untested, 0 tested, heuristic h0
      >>> g2 = GreedySearcher(h1)
      >>> g2
      GreedySearcher: 0 untested, 0 tested, heuristic h1
      >>> g1.heuristic(s1)   # g1 uses h0, so its heuristic always returns 0
      0
      >>> g2.heuristic(s1)   # g2 uses h1, so its heuristic returns h1's estimate
      5
      >>> g2.priority(s1)    # the priority is -1 times the heuristic value
      -5
      

   5. Write a method add_state(self, state) that overrides (i.e., replaces) the add_state method that is inherited from Searcher. Rather than simply adding the specified state to the list of untested states, the method should add a sublist that is a [priority, state] pair, where priority is the priority of state that is determined by calling the priority method. Pairing each state with its priority will allow a GreedySearcher to choose its next state based on the priorities of the states.

      Example:

      >>> g = GreedySearcher(h1)
      >>> s = State(Board('142358607'), None, 'init')
      >>> g.add_state(s)
      >>> g.states     # contains a sublist pairing s with its priority
      [[-5, 142358607-init-0]]
      >>> succ = s.generate_successors()
      >>> g.add_states(succ)   # call add_states, not add_state!
      >>> g.states
      [[-5, 142358607-init-0], [-5, 142308657-up-1], [-6, 142358067-left-1], [-4, 142358670-right-1]]
      

      Note that although it was necessary to override add_state (the method that adds a single state), you should not need to override add_states (the method that adds a list of states). This is because the original version of add_states should already call add_state to do the work of adding each state in the list of states, and thus it will end up calling the GreedySearcher version of add_state when it is used with a GreedySearcher object.

   6. Write a method next_state(self) that overrides (i.e., replaces) the next_state method that is inherited from Searcher. This version of next_state should choose one of the states with the highest priority.

      Hints:

      • You can use max to find the sublist with the highest priority. If multiple sublists are tied for the highest priority, max will choose one of them.

      • You should remove the selected sublist from states, and you should return only the state component of the sublist – not the entire sublist.

      Examples:

      >>> g = GreedySearcher(h1)
      >>> s = State(Board('142358607'), None, 'init')
      >>> g.add_state(s)
      >>> succ = s.generate_successors()
      >>> g.add_state(succ[1])
      >>> g.states
      [[-5, 142358607-init-0], [-6, 142358067-left-1]]
      >>> g.next_state()    # -5 is the higher priority
      142358607-init-0
      >>> g.states
      [[-6, 142358067-left-1]]
      

5. In searcher.py, define a class called AStarSearcher for searcher objects that perform A* search. Like greedy search, A* is an informed search algorithm that assigns a priority to each state based on a heuristic function, and that selects the next state based on those priorities. However, when A* assigns a priority to a state, it also takes into account the cost that has already been expended to get to that state (i.e. the number of moves to that state). More specifically, the priority of a state is computed using the following pseudocode:

   priority(state) = -1 * (heuristic(state) + num_moves)
   

   where heuristic(state) is the value that the searcher’s heuristic function assigns to the state, and num_moves is the number of moves that it took to get to that state from the initial state.

   Once again, you should take full advantage of inheritance. However, we’re leaving it up to you decide which class to inherit from and how much new, non-inherited code is needed!

   Here’s one thing you need to know: When constructing an AStarSearcher object, you will need to pass in the heuristic function, just as you do when constructing a GreedySearcher object. See below for an example of constructing one.

   Examples:

   >>> a = AStarSearcher(h1)
   >>> a
   AStarSearcher: 0 untested, 0 tested, heuristic h1
   >>> s = State(Board('142358607'), None, 'init')
   >>> a.add_state(s)
   >>> a.states          # init state has same priority as in greedy
   [[-5, 142358607-init-0]]
   >>> succ = s.generate_successors()
   >>> a.add_state(succ[1])
   >>> a.states         # succ[1] has a priority of -1*(6 + 1) = -7
   [[-5, 142358607-init-0], [-7, 142358067-left-1]]
   >>> a.next_state()   # -5 is the higher priority, so that state is chosen 
   142358607-init-0
   >>> a.states
   [[-7, 142358067-left-1]]
   

6. Modify the create_searcher helper function in eight_puzzle.py so that it will be able to create GreedySearcher and AStarSearcher objects. To do so, simply uncomment the lines that handle cases in which the algorithm input is 'Greedy' or 'A*'.

   After you do so, try using the eight_puzzle driver function to see how the informed search algorithms perform on various puzzles. Here are some digit strings for puzzles that you might want to try, along with the number of moves in their optimal solutions:

   • '142358607' - 5 moves
   • '031642785' - 8 moves
   • '341682075' - 10 moves
   • '631074852' - 15 moves
   • '763401852' - 18 moves
   • '145803627' - 20 moves

   A* should obtain optimal solutions; Greedy Search may or may not.

   Note: When you use the eight_puzzle() function to test your GreedySearcher and AStarSearcher classes, make sure to pass in a heuristic function as the third input, not a depth limit. For example:

   >>> eight_puzzle('142358607', 'Greedy', h1)
   >>> eight_puzzle('142358607', 'A*', h1)
   

   If a given algorithm ends up taking longer than you can afford to wait, you can stop it by using Ctrl-C from the keyboard.

Part V: Compare algorithms, and try to speed things up!

In this last part of the project, you will write code to facilitate the comparison of the different state-space search algorithms, and you will also attempt to speed things up so that your code can more easily solve puzzles that require many moves.

Your tasks

1. In eight_puzzle.py, write a function named process_file(filename, algorithm, param). It should take the following three inputs:

   • a string filename specifying the name of a text file in which each line is a digit string for an eight puzzle. For example, here is a sample file containing 10 digit strings, each of which represents an eight puzzle that can be solved in 10 moves: 10_moves.txt

   • a string algorithm that specifies which state-space search algorithm should be used to solve the puzzles ('random', 'BFS', 'DFS', 'Greedy', or 'A*')

   • a third input param that allows you to specify a parameter for the searcher – either a depth limit (for the uninformed search algorithms) or a choice of heuristic function (for the informed search algorithms).

   Your function should open the file with the specified filename for reading, and it should use a loop to process the file one line at a time. We discussed line-by-line file processing earlier in the semester.

   For each line of the file, the function should:

   • obtain the digit string on that line (stripping off the newline at the end of the line)

   • take the steps needed to solve the eight puzzle for that digit string using the algorithm and parameter specified by the second and third inputs to the function

   • report the number of moves in the solution, and the number of states tested during the search for a solution

   In addition, the function should perform the cumulative computations needed to report the following summary statistics after processing the entire file:

   • number of puzzles solved
   • average number of moves in the solutions
   • average number of states tested

   For example:

   >>> process_file('10_moves.txt', 'BFS', -1)
   125637084: 10 moves, 661 states tested
   432601785: 10 moves, 1172 states tested
   025318467: 10 moves, 534 states tested
   134602785: 10 moves, 728 states tested
   341762085: 10 moves, 578 states tested
   125608437: 10 moves, 827 states tested
   540132678: 10 moves, 822 states tested
   174382650: 10 moves, 692 states tested
   154328067: 10 moves, 801 states tested
   245108367: 10 moves, 659 states tested
   
   solved 10 puzzles
   averages: 10.0 moves, 747.4 states tested
   

   (In this case, because BFS finds optimal solutions, every solution has the same number of moves, but for other algorithms this won’t necessarily be the case.)

   Notes/hints:

   • You can model your code for solving a given puzzle on the code that we’ve given you in the eight_puzzle driver function. In particular, you can emulate the way that this function:

     • creates Board and State objects for the initial state
     • calls the create_searcher helper function to create the necessary type of searcher object, and handles the possible return value of None from that function

     Important: Make sure to create a new searcher object for each puzzle (i.e., for each line of the file). Otherwise, the searcher will still have information inside it from previous searches when it starts to solve a new puzzle.

   • When calling the searcher object’s find_solution method, you should do so as follows:

     soln = None
     try:
         soln = searcher.find_solution(s)
     except KeyboardInterrupt:
         print('search terminated, ', end='')
     

     Making the call to find_solution() in this way will allow you to terminate a search that goes on too long by using Ctrl-C. In such cases, soln will end up with a value of None (meaning that no solution was found), and you should make sure to properly handle such cases.

   • You should not use a timer in this function.

   • This function should not return a value.

   Testing your function:

   • If you haven’t already done so, download the 10_moves.txt file, putting it in the same folder as the rest of your files for the project.

   • Try to reproduce the results for BFS shown above.

   • Try applying Greedy Search to the same file. You may find that it takes Greedy a very long time to solve some of the puzzles, at least when using h1 (the num-misplaced-tiles heuristic). If this happens, use Ctrl-C as needed to terminate the problematic searches. When we processed 10_moves.txt using our implementation of Greedy, we ended up using Ctrl-C to terminate two of the searches:

     >>> process_file('10_moves.txt', 'Greedy', h1)
     125637084: 204 moves, 658 states tested
     432601785: 12 moves, 13 states tested
     025318467: search terminated, no solution
     134602785: 78 moves, 221 states tested
     341762085: 26 moves, 339 states tested
     125608437: 162 moves, 560 states tested
     540132678: 68 moves, 749 states tested
     174382650: search terminated, no solution
     154328067: 10 moves, 16 states tested
     245108367: 48 moves, 49 states tested
     
     solved 8 puzzles
     averages: 76.0 moves, 325.625 states tested
     

   • It’s also possible for none of the puzzles to have a solution, and you should handle that situation appropriately. For example, this can happen if you impose a depth limit that is too small:

     >>> process_file('10_moves.txt', 'DFS', 5)    # depth limit of 5
     125637084: no solution
     432601785: no solution
     025318467: no solution
     134602785: no solution
     341762085: no solution
     125608437: no solution
     540132678: no solution
     174382650: no solution
     154328067: no solution
     245108367: no solution
     
     solved 0 puzzles
     

     Note that you can’t compute any averages in this case, so you shouldn’t print the averages line in the results.

2. Create a plain-text file named results.txt, and put your name and email (and those of your partner, if any) at the top of the file.

3. Conduct an initial set of experiments in which you try all of the algorithms on the puzzles in the following files:

   • 5_moves.txt - puzzles that can be solved in 5 moves
   • 10_moves.txt - puzzles that can be solved in 10 moves
   • 15_moves.txt - puzzles that can be solved in 15 moves

   More specifically, you should run the following algorithms on each file:

   • random
   • BFS
   • DFS with a depth limit of 20
   • DFS with a depth limit of 50
   • Greedy (using h1 – the num-misplaced-tiles heuristic)
   • A* (using the same heuristic)

   Note that it may be necessary to use Ctrl-C to terminate searches that take too much time. You might want to pick a given amount of time (e.g., 30 seconds or 1 minute), and use Ctrl-C to terminate any search that doesn’t complete in that time.

   In your results.txt file, create three tables that summarize the results of these initial experiments. Use a separate table for each file’s results. For example, the results for 5_moves.txt should be put into a table that looks like this:

   puzzles with 5-move optimal solutions
   -------------------------------------
   algorithm                num. solved    avg. moves    avg. states tested
   ------------------------------------------------------------------------
   random
   BFS
   DFS (depth limit 20)
   DFS (depth limit 50)
   Greedy Search (using h1) 
   A* (using h1)
   

   Below these tables, write a short reflection (one or two paragraphs) in which you summarize the key points that are illustrated by the results. For example, you might discuss whether the algorithms produce reliably optimal results, and how much work they do in finding a solution. There’s no one correct reflection; we just want to see that you have reflected intelligently on the results and drawn some conclusions.

4. Even informed search algorithms like Greedy Search and A* can be slow on problems that require a large number of moves. This is especially true if the heuristic function used by the algorithm doesn’t do a good enough job of estimating the remaining cost to the goal.

   Our h1 heuristic function–which uses the number of misplaced tiles as the estimate of the remaining cost–is one example of a less than ideal heuristic. For example, consider the following two puzzles: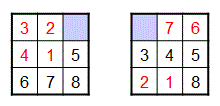

   

   Both of them have 4 misplaced tiles (the ones displayed in red), but the puzzle on the left can be solved in 4 moves, whereas the puzzle on the right requires 24 moves! Clearly, it would be better if our heuristic could do a better job of distinguishing between these two puzzles.

   Come up with at least one alternate heuristic, and implement it as part of your classes for informed searchers (GreedySearcher and AStarSearcher). To do so, you should take the following steps:

   1. As needed, add one or more methods to the Board class that will be used by your new heuristic function. (Adding a new method to the Board class is not required, but it can be helpful to add one so that the heuristic function can obtain the information needed for its estimate.)

   2. Add your new heuristic function(s) to searcher.py, and follow these guidelines:

      • Continue the numbering scheme that we established for the earlier heuristic functions. Call your first alternate heuristic function h2, your next heuristic function (if any) h3, etc.

      • Make sure that each heuristic function is a regular function, not a method. In addition, make sure that it takes a single State object and returns an integer.

   3. When conducting tests using a new heuristic function, use its name in the same ways that you would use h0 or h1. For example:

      >>> g = GreedySearcher(h2)
      >>> eight_puzzle('142358607', 'Greedy', h2)
      >>> process_file('15_moves.txt', 'A*', h2)
      

   You are welcome to design more than one new heuristic function, although only one is required.

   When testing and refining your heuristic(s), you can use the files that we provided above, as well as the following files:

   • 18_moves.txt - puzzles that can be solved in 18 moves
   • 21_moves.txt - puzzles that can be solved in 21 moves
   • 24_moves.txt - puzzles that can be solved in 24 moves
   • 27_moves.txt - puzzles that can be solved in 27 moves

   Compare the performance of Greedy and A* using the h1 heuristic to their performance using your new heuristic(s). Keep revising your heuristic(s) as needed until you are satisfied. Ideally, you should see the following when using your new heuristic(s):

   • Both Greedy and A* are able to solve puzzles more quickly – testing fewer states on average and requiring fewer searches to be terminated.

   • Greedy Search is able to find solutions requiring fewer moves.

   • A* continues to find optimal solutions. (If it starts finding solutions with more than the optimal number of moves, that probably means that your heuristic is overestimating the remaining cost for at least some states.)

5. Although you are welcome to keep more than one new heuristic function, we will ultimately test only one of them. Please adjust your code as needed so that the heuristic function that you want us to test is named h2. Also, please make sure that we will still be able to test the num-misplaced-tiles heuristic if we specify h1 for the heuristic.

   In your results.txt file, briefly describe how your best new heuristic works:

   heuristic h2
   ------------
   This heuristic ...
   

   If your code includes other alternate heuristics, you are welcome to describe them as well, although doing so is not required.

6. Conduct a second set of experiments in which you try both your new heuristic function(s) and the h1 heuristic function on the puzzles in the four new files provided above (the ones that require 18, 21, 24, and 27 moves).

   In your results.txt file, create four tables that summarize the results of these experiments. Use a separate table for each file’s results. For example, the results for 18_moves.txt should be put into a table that looks like this:

   puzzles with 18-move optimal solutions
   --------------------------------------
   algorithm              num. solved    avg. moves    avg. states tested
   ----------------------------------------------------------------------
   Greedy (heuristic h1)
   Greedy (heuristic h2)
   # Greedy with any other heuristics
   
   A* (heuristic h1)
   A* (heuristic h2)
   # Greedy with any other heuristics
   

   Below these tables, write a short reflection (one or two paragraphs) in which you summarize the key points that are illustrated by the results. Here again, there is no one correct reflection; we just want to see that you have reflected intelligently on the results and drawn some conclusions.

Submitting Your Work

IMPORTANT: Your work for Parts I and II should be submitted as part of Problem Set 10. See that assignment for more detail.

The following instructions are for submitting the full project, which should include your work on all parts of the project.

You should use Apollo to submit the following files:

• your final board.py file (even if you submitted the same version of the file for PS 10)
• your final state.py file (even if you submitted the same version of the file for PS 10)
• your searcher.py file
• your eight_puzzle.py file
• your results.txt file containing the results of your experiments from Part V

If you worked on one or more pair-optional problems with a partner, make sure that you each submit a copy of your joint work, and that you include comments at the top of the file specifying the name and email of your partner.

Here are the steps:

1. Login to Apollo, using the link in the left-hand navigation bar. You will need to use your Kerberos user name and your Apollo access code. If you have not yet registered for Apollo, follow the instructions on the registration page, which is linked to from the login page.
2. Check to see that your BU username is at the top of the Apollo page. If it isn’t, click the Log out button and login again.
3. Find the appropriate problem set section on the main page and click Upload files.
4. For each file that you want to submit, find the matching upload section for the file. Make sure that you use the right section for each file. You may upload any number of files at a time.
5. Click the Upload button at the bottom of the page.
6. Review the upload results. If Apollo reports any issues, return to the upload page by clicking the link at the top of the results page, and try the upload again, per Apollo’s advice.
7. Once all of your files have been successfully uploaded, return to the upload page by clicking the link at the top of the results page. The upload page will show you when you uploaded each file, and it will give you a way to view or download the uploaded file. Click on the link for each file so that you can ensure that you submitted the correct file.