Now that we know the design goals and the relevant implementation details of BRITE, in this section we provide a symbolic comparative study of some generation models. The idea of doing this comparison is to illustrate the design principles of BRITE in a ``real-world'' environment.
Recent empirical studies [9] have shown that Internet topologies
exhibit power-laws of the form
![]() for, among other
properties, (P1) the outdegree of a node versus rank, and (P2) frequency of
an outdegree versus outdegree. The seeming invariance of these properties
with respect to size and time suggests they are fundamental properties of
Internet topologies. After this discovery, the question to be asked, do the
currently used topology generators generate topologies that satisfy this
property? [16].
for, among other
properties, (P1) the outdegree of a node versus rank, and (P2) frequency of
an outdegree versus outdegree. The seeming invariance of these properties
with respect to size and time suggests they are fundamental properties of
Internet topologies. After this discovery, the question to be asked, do the
currently used topology generators generate topologies that satisfy this
property? [16].
Using BRITE, we generated topologies according to the RouterWaxman and RouterBarabasiAlbert models. In addition, we used the ImportFileModel to import GT-ITM flat, GT-ITM Transit-Stub, and NLANR topologies and output them into BRITE's format. In order to do the analysis intended here, it is not needed to import the GT-ITM and NLANR topologies since they can be read directly by BRIANA. For each topology, we plot two types of plots for property (P1) and property (P2).
For the (P1) property, we plot outdegree versus rank in a log-log plot. For the (P2) property, we plot the frequency of outdegrees versus outdegrees as done in [9].
Figures 11 and 12 show the results for two of the data sets used in [9].
Figures 13 and 14 show the results for one GT-ITM flat topology and one GT-ITM Transit-Stub topology, respectively.
Figures 15 and 16 show the results for the BRITE topologies using the RouterWaxman and RouterBarabasiAlbert models, respectively.
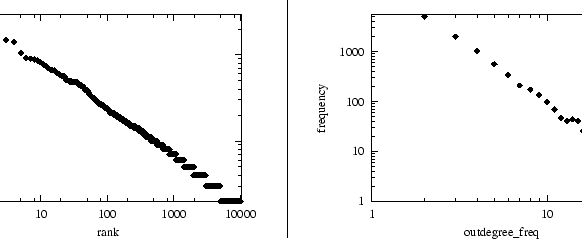 |
The goal of this section is not to make conclusive remarks with respect to the differences between the involved models/generators. However, we can see that when the Internet properties analyzed are the rank and frequency of node outdegrees [9], we can establish clear differences between generators aimed at reproducing degree-related properties (e.g. BRITE/BarabasiAlbert) and generators aimed at reproducing hierarchical properties (e.g. GT-ITM). In Figures 11 and 12 we observe the same type of results obtained in [9]. In Figures 13 and 14 we can observe that GT-ITM models lack some characteristic that would allow them to strike a balance between hierarchical properties and degree-related properties. Figure 15 shows that the Waxman model implemented in BRITE, aimed at generating random networks, fails in reproducing the outdegree distribution properties of the Internet topologies. Finally, Figure 16 shows that the BarabasiAlbert model implemented in BRITE does a fairly good job in reproducing the outdegree properties of Internet topologies [16].
We want to emphasize that this symbolic comparative study was performed in about 20 minutes using BRITE and BRIANA. Even when the goal was not to reach conclusions from the comparisons, this exercise illustrates how the principles of BRITE and BRIANA translate into an increased efficiency and productivity in the generation and analysis of topologies.