[About DWCS ][How DWCS Works ][DWCS Features ][Download
]
[Installation
][Using DWCS ][To Do
][Related Papers ][Related Web Sites ]
Change Log
- June 03, 2004: DWCS has been suspended while a new virtual deadline scheduler, that supercedes DWCS, is being developed. Time-permitting, DWCS patch files for recent Linux kernels will be added.
- New links will be added to a page on "Virtual Deadline Scheduling" that orders tasks (e.g., packets or threads) according to a function of current window-constraints and proportional fairness requirements. In the meantime, please check the paper list below.
- June 11, 2002: After a long period of inactivity, the Linux DWCS work is being resumed (albeit in limited capacity).
- Certain boundary conditions can force the scheduler to perform sub-optimally for processes with fixed-sized timeslices. From a theoretical standpoint, optimality is guaranteed only for canonical service constraints on processes. User-controllable support for conversion of service constraints to their canonical form will be incorporated into any future releases of the scheduler, one of which is hopefully a Linux-based packet scheduler.
- July 28, 2000: DWCS version 1.2 released. Major bug fixes and improvements include:
- /proc/dwcs enhancements. The /proc/dwcs code has been rewritten using the VFS functionality, by supplying functions to handle open(), close(), permissions(), and most importantly, a new version of read(). The advantage of this approach is that now we're not restricted to only passing back at most one memory page of statistical information to the user. Instead, as much information as necessary can be passed back to the user.
- 0/0 window-constraints now work, thereby enabling the scheduler to run as a pure EDF scheduler. In previous versions, this would cause a divide-by-zero error.
- Added `jiffies_last' to prevent DWCS updating service constraints multiple times in one jiffy. This was happening if schedule() was invoked more than once in one jiffy.
- Fixed bug in that if DWCS_WORK_CONS is set FALSE, a process cannot be scheduled multiple times in the same request period.
- November 1, 1999: DWCS version 1.1 released. New features include:
- SMP-compliant.
- Potential floating-point problems now fixed. DWCS is now implemented as a pure integer-based algorithm.
- Cleaner integration of the DWCS source code with the rest of the linux source tree.
- Simpler installation procedure. A
configuration entry has been added to the "Kernel Hacking"
menu to
enable/disable the building of the DWCS scheduler module.
Enabling the
compilation of the
DWCS scheduler allows an entry in the /proc filesystem to
be
configured,
showing the current state of DWCS scheduled processes.
- August 19, 1999: DWCS version 1.0 released for Linux 2.2.7.
- Thanks to Ivan Ganev for help on versions 1.1 and 1.2. Thanks also to Christian Poellabauer for past discussions on the algorithm itself.
What is DWCS?
Background. DWCS stands for Dynamic Window-Constrained Scheduling. Originally, DWCS was designed to be a network packet scheduler, that limited the number of late or lost packets over finite numbers of consecutive packets in loss-tolerant and/or delay-constrained , heterogeneous traffic streams. For example, virtual environments, tele-medicine, and real-time multimedia applications (including video-on-demand and streamed audio) can tolerate a certain fraction of late or lost information, without any noticeable degradation in the quality of playback at the receiver. However, it is important that such applications do not suffer losses at certain points in time, even though they can tolerate a certain fraction of information being lost. For most loss-tolerant applications, there is usually a restriction on the number of consecutive packet losses that are acceptable. For example, losing a series of consecutive packets from an audio stream might result in the loss of a complete section of audio, rather than merely a reduction in the signal-to-noise ratio. A suitable performance measure in this case is a windowed loss-rate , i.e. loss-rate constrained over a finite range, or window, of consecutive packets. More precisely, an application might tolerate x packet losses for every y arrivals at the various service points across a network. Any service discipline attempting to meet these requirements must ensure that the number of violations to the loss-tolerance specification is minimized (if not zero) across the whole stream. As a packet scheduler, DWCS attempts to meet windowed loss-rates for multiple packet streams, each with their own performance objectives.More recently, we have applied DWCS to scheduling processes (and threads) for execution on available CPUs of a host machine. In its current incarnation as a CPU scheduler, DWCS can guarantee that no more than x deadlines are missed every y deadlines, for a given process (or thread).
Real-Time CPU Scheduling. Many
scheduling policies have been used for real-time scheduling,
including cyclic executives, static priority algorithms
(such as
Rate-Monotonic Scheduling), and dynamic algorithms, such as
Earliest
Deadline First (EDF). Static priority algorithms all consider
that one
process (or thread) is more important to service than
another
process, based solely on each process's time-invariant
priority.
However, such algorithms do not take into account the
importance of
servicing a process can vary with time. Moreover,
real-time
systems require processes to complete their service by
specific
deadlines, in
order to meet necessary timeliness constraints. Consequently,
Earliest
Deadline First scheduling (EDF) considers that each
process's
importance (or priority) increases as the urgency of
completing that
process's service increases. That is, it is more
important to
service a process closer to its deadline than another process
further
from its deadline. Although EDF considers a process's
importance varies
with time, it does not consider that at any point in time, the
individual importance of two or more processes with the same
deadline
may be different. That is, if two processes have the
same
deadline, one process may require precedence over another, as
in static priority schemes. Furthermore, EDF assumes that the
urgency
of
servicing each process increases at the same rate for all
processes.
This is not true in all systems. Hence, there is a need for an
algorithm to combine both static priority and earliest
deadline first
properties. DWCS is one such
algorithm that combines both these properties. In fact, DWCS
can
perform static
priority, earliest deadline first, and real-time
proportional (or
"fair")
scheduling.
Real-Time Scheduling with DWCS
Background. The original DWCS packet scheduler required two service constraints to be specified for each packet stream. These were a maximum inter-packet gap (from which a per-packet deadline could be derived) and a loss-tolerance. For CPU scheduling, these terms were not so meaningful, so we changed the inter-packet gap to be a request period and the loss-tolerance to be a window-constraint.For CPU scheduling, a process has attributes in terms of a request period and a window-constraint . A request period defines an interval (window of time) over which a process must receive some share of the CPU. The end of one request period and the start of the next, for any given process, denotes a deadline. Hence, DWCS derives deadlines for each process, such that a process's current deadline is at the end of its current request period. The window-constraint is actually a fraction, x/y , and states that a process can miss being serviced at most x request periods out of every y request periods. That is, a process can miss x deadlines for every fixed window of y deadlines that are derived from its request period and current time. Observe that a process does NOT have to be a periodic process to use DWCS. For periodic processes, a request period can identify a window of time over which one instance of a process must executes to completion, before the next request for the same process requires servicing. For aperiodic processes (for example, processes that only execute once) , a request period identifies a window of time in which part of a process must execute. That is, for an aperiodic process, P, the current request period identifies the interval of time in which one timeslice (or service quantum) of P must execute, otherwise the current timeslice of P will miss its deadline. Consequently, the window-constraint of P specifies that up to x timeslices of P can be serviced late (outside their request periods) for each consecutive y timeslices. Clearly, a process, P , has a number of timeslices, dependent upon its overall service time. With DWCS, the size of each timeslice can be specified as some multiple of the system clock. For Intel platforms, the minimum timeslice for a process is 10mS , with larger timeslices being some multiple of 10mS, but this will change if we use the UTIME package from Kansas University. Moreover, each timeslice for a process (be it the time to service a full instance of a process, or simply part of that process) can be preemptible in a given request period.
Example. A process requires 50mS of service every request period of 100mS, tolerating 2 out of 10 missed service intervals. If timeslice preemption is enabled, that 50mS can be divided into 10mS units of CPU time, as long as a total of 50mS of CPU time is granted to this process every 100mS (with the exception of two intervals of 100mS in which the process can miss being serviced altogether). This process is said to have a window-constraint of 2/10, which implies that over every window of 10*100mS, the process can tolerate not being serviced for 50mS in two of its 100mS request periods. The minimum utilization for this process is:
U_min = (1 - x / y) * C / T, where C = 50mS of service time, T
= 100mS
for the request period, and x / y = 2/10 for the
window-constraint.
That is, U_min = 0.4 (or 40%)
For servicing at the granularity of the smallest (10mS) timeslice, we can consider the service constraints are:
C' = C / 5 = K (i.e., 10mS), T' = T / 5, and x' / y' = x / y.
Then, U_min' = (1 - x' / y') * K / T' = 8/10 * 10mS / 20 mS =
0.4
(or 40%)
How DWCS Works
DWCS is a relatively simple algorithm. It compares pairs of processes (or, equivalently, threads, or network-bound packets) and selects the highest priority process for service based on the following table of precedence rules:|
|
|
Earliest deadline first
(EDF)
|
|
|
|
|
|
|
|
|
Observe that the above table of precedence rules is not always optimal. That is, there are cases when the minimum required utilization of a set of processes to meet all window-constraints is less than 100% (meaning resources are available) but some processes will violate their window-constraints when serviced according to the above precedence rules. To deal with this case, each process' service constraints must be converted to their canonical form which yield equivalent minimum utilization demands, albeit over finer-grained windows of time. In most cases, this is actually preferable.
Canonical Service Constraints
To guarantee a feasible schedule, whereby all process' window-constraints are met as long as the total minimum utilization is less than 100%, original service constraints must be converted to their canonical form. This is because sub-optimal process schedules may result using a pairwise ordering method that considers deadlines before window-constraints (or vice versa).For any process, Pi, with service constraints, (Ci, Ti , xi / yi), representing service time, request period and window-constraints, respectively, we can perform an O(1) conversion to the canonical service constraints, (Ci', Ti', xi' / yi') as follows:
Ci' = Ci
Ti' = K
xi' = yi * (qi - 1) + xi
yi' = qi * yi
Assuming Ti = qi * K, Ci <= K for some constant K and positive integer, qi. This assumption is based on the notion that the system performs scheduling at the granularity of fixed-sized time-slots, that are K time units in length. In effect, this limits a timeslice to a maximum of K time units also.
Observe that 1 <= i <= n, if there are n processes, P1...Pn. Moreover, if:
sum (for all i) (1 - xi / yi) * Ci / Ti <= 1.0 then the minimum total utilization of the canonical constraints is no more than:
sum (for all i) (1 - xi' / yi') * K / Ti' <= 1.0 = U_min_total
The canonical service constraints ensure that no process violates its original window-constraints of xi / yi if U_min_total <= 1.0 .
Dynamic Service Constraint Adjustment
For each process serviced for at least one timeslice before its
deadline (i.e. a process that is serviced in its current request
period), the window-constraint x/y is
adjusted dynamically as follows, to, in effect, reduce the
urgency of
servicing the same process again when another more "critical"
process
requires service:
Let x be a process's original window-numerator, while y
is its original window
denominator. These are the values first set for a DWCS
process.
Let x' and y'
denote the current window numerator and current window
denominator as the process is
executed. Then, if a process is serviced before its deadline:
(A)
if (y' > x') then y' = y' - 1;
else if (y' == x') and (x' > 0) then x' = x' - 1; y' = y' - 1;
if (x' == y' == 0) or (the process is tagged with a violation. i.e. DWCS_VIOLATION is set) thenx' = x;if (the process is tagged with a violation) then
y' = y;reset DWCS_VIOLATION flag;
For any process not serviced by its deadline (i.e. its next
timeslice
has not been serviced in its latest request period) then:
(B)
if (x' > 0) thenx' = x' - 1; y' = y' -1;else if (x' == 0) and (y > 0) then
if (x' == y' == 0) thenx' = x;
y' = y;y' = y' + 1;
Tag process with a violation by setting its DWCS_VIOLATION flag;
The pseudo-code for DWCS is as follows.
It's actually more complicated than this but this will give
you a basic
understanding of what is happening to your processes:
Let Pi = ith process
di = deadline of Pi
Ti = request period
of Pi
Wi' = current window-constraint
of Pi
while (TRUE) {for (each process whose ready time <= current time)}find process, Pi, with the highest priority, according to the rules in the Table above;service next timeslice of Pi (which may mean servicing all of Pi);
adjust Wi' according to the rules in (A), above;
di = di + Ti;
for (each process, Pj, missing its deadline) {while (deadline missed) {}adjust Wj' according to the rules in (B), above;}
dj = dj + Tj;
Observe that a process with an original window-constraint of 0/0 actually forces the scheduler to treat it as a deadline-constrained process, whose deadline is calculated from the current time and the request period. Observe also (from the table), that deadlines are used as the primary means of deciding whether to service one process or another, every time the scheduler runs. In practice, you might think very few deadlines are actually equal, so why do we need all these extra decision rules? Well, in practice, it is unlikely that you would want to context switch from one process to another too frequently, because (a) the advantages of caching recently used instructions and data in the processor's cache are defeated, and (b) the context-switching overhead is too great. Therefore, most processes will probably want to run for longer (non-preemptive) periods of time. If this is the case, it makes sense to round a process's deadline to the nearest possible preemption point that is actually less than or equal to the real deadline. In doing this, chances are that more deadlines will be equal as the size of a non-preemptive timeslice is increased. The process can still be set to execute in entirety, or in part, depending on the size of a process's timeslice. (See sched_setscheduler , below, for details on how to adjust the size of a process's timeslice. This actually involves setting the service_time field of struct sched_param ). Below is a simple example of DWCS scheduling three processes, P1, P2, and P3, each with a timeslice of 1 time unit (which may well be 10mS or 10 seconds in reality). Each process has a request period of 1 time unit and the original window-constraints are 1/2, 3/4, and 6/8. Since each process has a request period of 1 time unit, each process has a new deadline every time unit also. In this example, let P1 comprise of 8 timeslices, while P2 and P3 each comprise of 4 timeslices. Below the time axis is a list of current window-constraints and deadlines for each process. Deadlines are shown in brackets. Over the full 16 time units, P1 receives 8 time units of service, while P2 and P3 both receive 4 time units of service. Moreover, P1 is serviced once every 2 time units, while P2 and P3 are serviced once every 4 time units. Therefore, P1 has not missed more than one deadline every two deadlines, and P2 and P3 have not missed more than 3 deadlines every window of 4 deadlines. In fact, P3 has weaker window-constraints, in that it requires that no more than 6 deadlines are missed every 8 consecutive deadlines (or, equivalently, 8 consecutive request periods). As it turns out, over the smallest possible window of time (4 time units), P1 receives twice has much service as P2 and P3. Hence, real-time proportional (or "fair") service is granted to all processes in proportion to their original window-constraints and request periods.
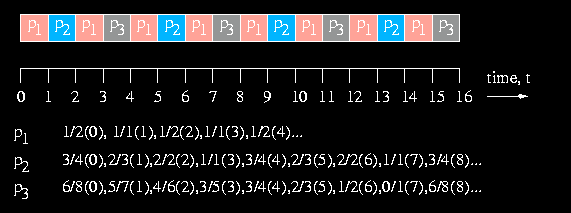
DWCS Scheduling Modes and Features
- Running DWCS in EDF mode: Ensure all process's have 0/0 window-constraints and request periods that are not -1.
- Running DWCS in static priority mode: Ensure all processes have request periods of -1 and then the value of the window-constraint specifies its priority. The process with the lowest window-constraint, x/y, has the highest priority.
- DWCS can run in mixed mode (with a combination of static priority and deadline-constrained processes), but beware that non-time-constrained (static priority) processes will not run if a time-constrained process is runnable. That is, a non-time-constrained process is any process whose request period is -1.
- By default, all system processes (e.g. telnetd, klogd, and related processes, such as an X-server) all run in non-time-constrained, static priority mode. However, these processes can be switched into time-constrained mode using dwcs_setscheduler (see below), so that they receive real-time service. NOTE: Due to the non-real-time nature of the standard Linux kernel, the real-time guarantees provided by DWCS will only be "soft" real-time guarantees. This is due to factors other than the scheduling policy. Work is underway to see how well a Linux-based system, employing DWCS, can meet real-time service constraints.
- Observe that, in Solaris, which has fixed priority classes, for system, real-time and timesharing processes (actually threads), the Solaris system processes can be prevented from receiving any service, if a real-time process is always runnable and never blocks on some wait condition. However, DWCS can provide proportional share, real-time service to processes, so that each process is guaranteed some fraction of CPU time over finite intervals of time. The actual amount of service to each process is in direct proportion to each process's window-constraints and request period.
- We have actually proven (theoretically) that if each process, Pi, requires a fixed quantum of service, Qi , (i.e. a fixed timeslice) in each request period, Ti , then if the sum of the worst-case minimum service demands from each process is less than 100% , each process is guaranteed to be serviced (1-Wi)Q*10mS every window of Ti*10mS , where Wi is the window-constraint of Pi. That is, each process has a worst-case minimum demand for service of (1-Wi)Q*10mS/Ti*10mS . If the sum of all processes' worst-case minimum demands for service is 1.0, the CPU will be 100% utilized (i.e. it will never be idle). However, DWCS guarantees that no process will violate its original window-constraint by ensuring each process's minimum demand for service every window, Ti*10mS . NOTE: These times assume the scheduler is not invoked by some means other than by a timer interrupt , and ignores interrupt and dispatch latencies. Saying this, we now want to prove possible service guarantees offered by DWCS for processes having variable-length service-times (i.e. variable-length timeslices) in every request period.
Where can I get DWCS?
- linux_2.2.7_dwcs_v1.2.tar.gz .This is the latest version for Linux 2.2.7, Intel machines, and should work on both SMP and non-SMP configured machines.
- linux_2.2.13_dwcs_v1.2.tar.gz
.This is the latest version for Linux 2.2.13, Intel
machines, and should work on both SMP and non-SMP configured
machines.
Linux 2.2.13 is the final 2.2.x kernel to be patched. Patches for recent Linux kernels may be available upon request. - linux_2.2.7_dwcs_v1.0.tar.gz . This version is for Linux 2.2.7, Intel machines. This version does not work on SMP machines. You should disable SMP support to be sure that this code works correctly.
- linux_2.2.7_dwcs_v1.1.tar.gz . This version is for Linux 2.2.7, Intel machines, and should work on both SMP and non-SMP configured machines.
- linux_2.2.13_dwcs_v1.1.tar.gz . This version is for Linux 2.2.13, Intel machines, and should work on both SMP and non-SMP configured machines.
The following gzip'd tarfiles are now obsolete and are only here for completeness. Unless you are really curious, you should use the latest versions above.
Installation Notes
1. Download a copy of the tar file and unpack its contents by typing:
gzip -dc linux_2.2.*_dwcs_v1.*.tar.gz | tar xvf - (where * is replaced with the appropriate version number)
2. Read the INSTALL file in the newly-created dwcs directory.
Using DWCS
- DWCS is a kernel loadable module. As root, you must type modprobe dwcs (or depmod -a; modprobe dwcs or , if all else fails, insmod dwcs ) to load the DWCS extensions into a running Linux kernel.
- To enable DWCS once the dwcs module has been loaded, type load_scheduler.
- To disable DWCS after it is the active scheduler in the Linux kernel, type unload_scheduler.
- At any point in time, it is safe to remove the DWCS kernel loadable module by typing rmmod dwcs . Removing the module will return the system to using the default Linux (timesharing) scheduler.
- If you type cat /proc/dwcs when the dwcs module is loaded, you can see a snapshot of the DWCS scheduling parameters for processes currently on the scheduler's runqueue. If there's not much there, that's because most processes are blocked. Check 'top' to verify the number of processes actually using the CPU at the current time.
- You can now use the sched_setscheduler call within your programs to set the service constraints on real-time DWCS processes. An example of how to adjust the service constraints of a DWCS process, using sched_setscheduler, is as follows:
- The modifications to struct sched_param can be found in schedbits.h and sched.h, included with the downloadable tarfile. Depending on your Linux distribution, either schedbits.h or sched.h will replace your existing /usr/include/schedbits.h or /usr/include/bits/sched.h file. A similar file in the linux source tree, linux/sched.h , is also modified to include the DWCS scheduling parameters.
#include <sched.h>
#include <sys/types.h>
#include <unistd.h>
/* DWCS_WORK_CONS is set when a process supports
work-conservation. */
#define
DWCS_WORK_CONS
0x00000002
/* DWCS_NON_PREEMPTIVE is set when a
process must execute with non-preemptive
timeslices. */
#define DWCS_NON_PREEMPTIVE 0x00000004
int main (int argc, char *argv[]) {
-
struct sched_param sp;
int pid;
pid = getpid();
/* sp.period is
multiplied by 10mS to get the actual scheduling period. */
sp.period = 5;
/* sp.own is the original
window numerator. This is the value x in
the window-constraint x/y . */
sp.own = 1;
/* sp.owd is the original
window denominator. This is the value y
in the window-constraint x/y . */
sp.owd = 100;
/* sp.flags : Can logical OR
the flags DWCS_WORK_CONS and DWCS_NON_PREEMPTIVE. If
DWCS_WORK_CONS is set, then potentially multiple
timeslices of
a given process can execute in a single request period.
This will only
happen if all other deadline-constrained processes have
been serviced
in their current request period. If DWCS_NON_PREEMPTIVE is
set, then a timeslice must execute
without preemption in
each request period. NOTE: A non-preemptive timeslice will
currently
execute
at least 10mS. */
sp.flags = 0;
/* sp.service_time is currently a number that is
multiplied by 10mS to
determine the maximum amount of service time each
timeslice of a
process should receive in one request period. This can be
sufficiently
large to cover the time to service the whole process, in
the case of a
periodic process, for example, or can be the time to
service part
of a process in one request period. If DWCS_NON_PREEMPTIVE
is not set, then this
service time can be preempted every time the
scheduler executes, to allow other processes' timeslices
to execute.
However,
DWCS will still attempt to service a process for
sp.service_time*10mS
every sp.period*10mS, except where the process's
window-constraints allow
timeslices to skip being serviced in corresponding request
periods. */
sp.service_time = 2;
if ((ret = sched_setscheduler (pid, SCHED_DWCS, &sp)) < 0)
-
fprintf (stderr, "Error setting scheduling
attributes!\n");
- A command-line executable, dwcs_setscheduler , allows the service constraints of running processes to be altered from a shell. It is essentially a small program that utilizes sched_setscheduler, just as in the above example. dwcs_setscheduler takes 4 mandatory arguments and 2 optional arguments, as follows:
- pid - this is the ID of the process whose service constraints are to be altered.
- period - the request period (specified as some number which is multiplied by 10mS).
- own - the original window numerator, which is the value x in the window-constraint, x/y.
- owd - the original window denominator, which is the value y in the window-constraint, x/y.
- -s <service_time> - this is the amount of service for a process's timeslice per request period. It is a number which is multiplied by 10mS to get the actual service time. The default service time for one timeslice is 10mS, so the service_time field of struct sched_param defaults to 1.
- -f <flags> - this value sets the flags field of struct sched_param . The default value is 0. Each new value of flags can be set by OR-ing the new value with the old value. Currently, only DWCS_WORK_CONS and DWCS_NON_PREEMPTIVE are acceptible flags. These can be entered on the command line, separated by a comma, if both flags are to be set. See the example above for a description of the meaning of these flags.
-
The following arguments are optional:
To Do
- Add DWCS packet scheduling to Linux.
- Add an on-line admission control (or scheduling analysis) module to work with DWCS packet and CPU scheduling.
- Add UTIME (Kansas University) microsecond timer support, for fine-grained timeslices.
- This work is part of the Dionisys QoS Adaptive System work at Georgia Tech. We hope to port the Dionisys QoS Infrastructure to Linux and, hopefully, embed some of its components into the kernel, to ultimately implement a distributed, real-time adaptive system that adapts communication and computation resources, in terms of CPU and network (primarily bandwidth) resources. Dionisys is being prototyped on Solaris and Linux in user-space, along with the original DWCS packet scheduler, which was first implemented in shared memory.
- Add real-time events (RTE) to Linux to allow DWCS CPU and packet service managers to communicate, thereby supporting true hierarchical scheduling between the host computer and the network.
Selected Papers
|
[pdf][ps.gz] |
|
[pdf][ps.gz] |
|
[ps.Z][pdf][ps] |
|
[pdf][ps.gz] |
|
[pdf][ps.gz] |
|
[pdf][ps.gz] |
|
[pdf][ps.gz] |
|
[pdf][ps.gz] |
Presentations
|
[pdf] |
|
[pdf] |
|
[pdf] |
|
[pdf] |
|
[pdf] |
|
[pdf] |
Related Web Sites
This page is maintained by Rich West (richwest@cs.bu.edu )