Analysis and Simulation of a Fair Queuing Algorithm
1) Definitions:
a) Per Flow Queuing:
In Per Flow queuing, routers maintain state
for each flow, ie. the flows are segregated. In previous algorithms (ex.
FIFO) , the queues were indifferent to the various flows. The only exception
was RED were the amount of packets dropped was proportional to the flows
bandwidth.
b) Queue Management vs. Queue Scheduling:
Queue management consists of algorithms that decide
which packets get dropped. On the other hand, queue scheduling is concerned
with which packets get transmitted and when do they get transmitted.
c) Work Conserving:
Do work if there is work to be done, ie. if there
are packets in the queue directly service them
d) Max-Min Fairness:
The Max-Min fairness index represents an alternative
index to that proposed by Ciu and Jain. In the Max-Min index, all users
have equal rights to the resource (queue). Fairness is acheived if user
can increase his utilization of the resource without decerasing the utilization
of someone with a lesser or equal allocation.
The following example illustrates the idea:
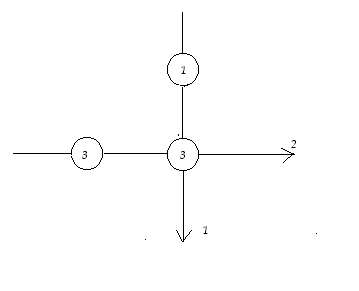
The first flow needs a bandwith of 3. The second one needs 1. The bottleneck
bandwith is 3. We start by allocating 1.5 to each user. Howerver the second
on can only use 1, therefore we give it the 1 it requires and add the remaining
0.5 to the first user. The basic idea is to share the available BW as fairly
as possoble. If there is residue, we give it to someone who can use it.
2) Fair Queuing:
In Fair Queuing, Max-Min index is used. Obviously, the most fair algorithm
is the bit-by-bit round robin algorithm, where one bit of each flow is
serviced per round. However it's not practical. Nagle suggested a packet-by-packet
round robin solution. The main drawback of his algorithm is that it does
not take into account the size of packets, therefore a flow with small
size packets will recieve less bandwidth than one with large packet size.
As a solution, the Fair Queuing Algorithm was proposed. Its main objective
is to try to emulate the bit-by-bit round robin algorithm on a packet by
packet basis.
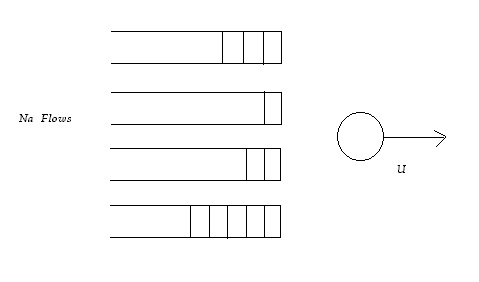
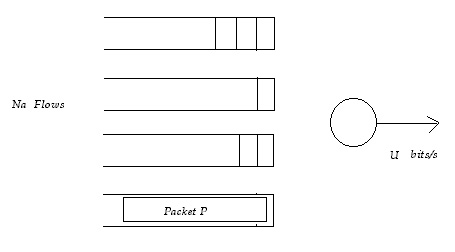
Na is the
number of active flows
u is the available bandwidth
R(t)= # of rounds that
bit-by-bit round robin would have performed by time t ( could be a fraction).
The idea is to use R(t) as the clock instead of using
time, ie. the time of arrival of a packet for example would be R(t) instead
of t.
For each arriving packet, we calculate its finish
time ( R(tf) ). Then, we forward the packet with the smallest finish time.
Also, notice the following relation :
dR(t) / dt= u / Na
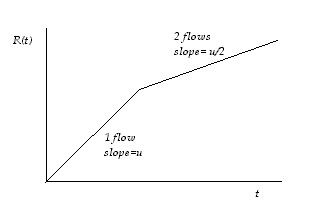
As the number of flows increases, slope of R(t) decreases ( In
bit-by-bit, the number of rounds performed in a time interval decreases
because the queue has to service more bits per round).
Case 1) Empty Queue:
Suppose that a packet P arrives at to to an empty queue.
R(to) is the arrival time
R(tf) is the departure time
P is the packet size
=> R(tf)=R(to)+P
Consider the following example:
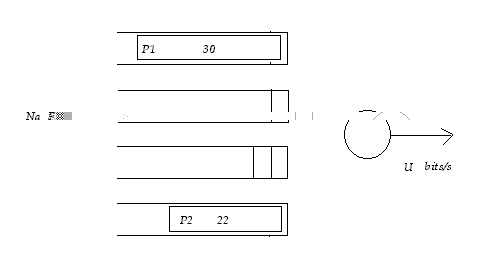
P1 arrives at to
R(to)=12
P1=10 bits
=> R(tf)=22
P2 arrives earlier at another queue.
R(to)=0
P2= 30 bits
=>R(tf)=30
Since the finish time of the first packet is smaller, we service it
first. It is clear that under bit-by-bit, the first packet would have finished
earlier.
* The conclusion is that the ordering of finishing times in fair queuing
is the same as that of bit-by-bit.
Case 2) Full Queue
If P arrives to a full queue, then the previous packet must finish before
starting to service P. Therefore the finish time of the previous packet
must be taken into account.
General Case)
In general, for a particular flow:
Fi= finish time of packet i
Si= start time
P= packet size
Si=Max(Fi-1, R(t))
and Fi=Si+P
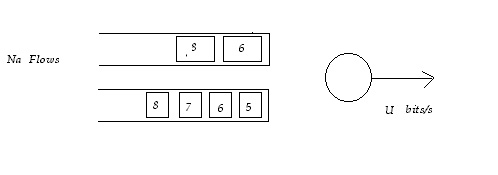
Example:
R(to)=4
2 packets for C1 of size 2 arrive at to
4 packets for C2 of size 1 arrive at to
The following figure shows the calculated finish times for each packet.
According to these times, we service the packets in an increasing order
( C1 is the flow in the top queue).
Another Goal:
Another goal of the Fair Queuing algorithm is to give more promptness
to users with less than their fair share.
This can be achieved by using another variable , the Bid B instead of
the finish time when determining which packet to forward.
Where
Bi= Pi+ Max( Fi-1, Si- d)
For users heavily utilizing their bandwidth, Fi-1
term dominates. However for idle users, the Si-d term gives preference
to users who have been idle for up to d timestamps.
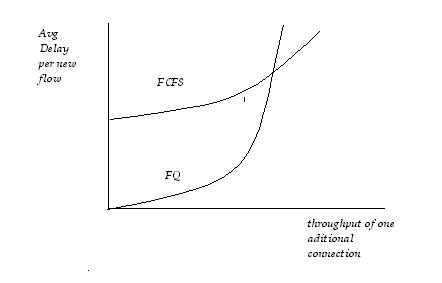
Performance:
The following figure shows the performance of Fair Queuing as opposed
to FIFO queuing. It is obvious that when the new flow is using less than
its fair share under FQ, it experiences less delay.
Generalized Prcessor Approach
This paper demonstrates that using Weighted Fair Queuing in addition
to the Leaky Bucket Admission Control, worst case performance guarantees
(BW, delay) can be achieved.
WFQ+ Leaky Bucket => Worst case guarantees (BW, Delay).
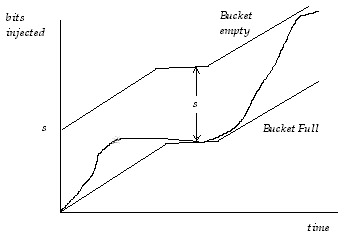
1) The Leaky Bucket Admission Control
The role of the leaky bucket is insure that before entering the queue,
traffic is shaped and controlled. It regulates the traffic entering the
network.
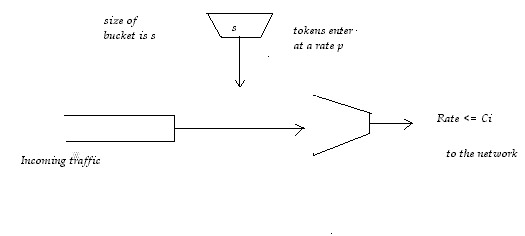
The tokens are generated into the bucket at a rate p. The size of the
bucket is s. Each incoming packet can not proceed before using up a token.
When the bucket is full, no more tokens are produced. This way, the max
amount of traffic injected to the network at ant time is restricted to
s. This way, burstiness is controlled.
The following figure shows how the output of the packet is restricted
between the 2 lines corresponding to an empty bucket and a full bucket.
Also the slope of the admission rate is less than the peak rate C.