Lab 12: Finite-state machines

Task 0: complete lab evaluations
Task 1: Find logic errors in functions
Task 2: practice using JFLAP
Task 3: design your own FSM
Extra-practice exercise

Task 0: complete lab evaluations

We will begin by taking a few minutes to complete evaluations for the lab component of the course.

These evaluations are only for the TAs. There is a separate evaluation of the undergraduate course assistants that you will complete later, so please don’t comment about the CAs on today’s form.
You should also leave any questions about the lecturer blank, since there will be a separate evaluation for the lectures.
Your evaluations are anonymous, and we will not receive the results until after all final grades have been submitted.
Comments in the text fields are valued and encouraged. Please try to answer all questions, but if a question is not applicable or you do not wish to answer it, you can simply skip it.

Here is the URL that you should use: https://bu.bluera.com/bu/

Enter your BU login name and Kerberos password, and complete the evaluation for your CS 111 lab section (the one with the section number that the TA will provide). Please do not evaluate your lecture section at this time.
When you are done with the survey, please close the separate browser tab.

Thanks in advance for taking the time to provide your feedback about the labs!

Task 1: Find logic errors in functions

Before working with FSMs, let’s take a few moments to consider the following two functions, each of which has a serious logic error. Find the errors. Note: You should be able to find the issues without even knowing what the functions are supposed to do!

def func1(vals, y):
    """ takes a list of integers vals and a single integer y """
    for x in vals:
        if x % y == 0:
            return x
        else:
            return 0


def func2(vals, y):
    """ takes a list of integers vals and a single integer y """
    result = 0
    for x in vals:
        if x % y == 0:
            result += x

    return result

    if result == 0:
        return -1

Task 2: practice using JFLAP

In Problem Set 10, you will use tool called JFLAP to build and test several finite state machines.

If you have already installed the necessary software, you can use it during this lab.

If you haven’t installed the software, you should draw the FSMs on paper for now. Later, you can install the software and consult the troubleshooting information provided as needed. You can also use JFLAP on the virtual desktop.

Consider the following FSM:

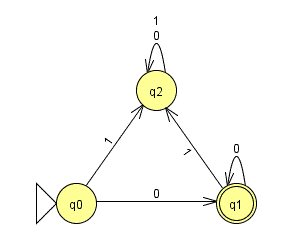
Which state is the start state?
Which state(s) are accepting states?
How many outgoing transitions does each state have? Is this required?
Which states(s) are “black hole” states – i.e., states that, once you enter them, you can never leave? Will you always need that type of state in your FSM? When is it useful?

Now let’s work together to create this FSM in JFLAP.

Click on the button for Finite Automaton and save your work in a file named lab12task2.jff.

Use JFLAP to test the following inputs:
- 0
- 10
- 111
- 00000
Which of them are accepted and which are not?

If you get stuck while working with JFLAP, there’s an online tutorial that can be found here. Because we’re only working with deterministic FSMs, you should limit yourself to the first 7 sections of the tutorial.

Warnings

In the FSMs that you construct for this problem set, each state should have exactly one outgoing transition for 0 and exactly one outgoing transition for 1.
When you want two different characters to act as transitions from one state to another state, be sure to draw two different edges and provide each transition character separately. JFlap will stack the transition characters on top of each other, as you see in the image above. If you use a comma or otherwise try to input both characters at once for a single edge, JFlap will think you want all of that text to be the transition, instead of the individual characters. (JFlap supports multi-character transitions, but you won’t want them for the problems we will be solving.)

Task 3: design your own FSM

If you are using JFLAP, click on the button for Finite Automaton. Save your work in a file named lab12task3.jff. You can also do the work for this task on paper.

Build a deterministic finite-state machine that accepts all bit strings containing the pattern 010, and that rejects all other bit strings.

This problem requires at least four states. You may use more states if necessary (there’s no penalty for doing so), but if you have time, try to get as close to the minimum as possible!

Here are three examples of strings that should be accepted:

010
1101001110001
001011

Here are three strings that should be rejected:

01
110110
0001111

Important

You should try convince yourself through logical reasoning that your FSMs correctly handle all possible inputs. The fact that a given FSM correctly handles all of the test cases that we’ve provided does not necessarily means that it works in general. We will be using additional test cases when grading the FSMs that you submit as part of Problem Set 10.

Extra-practice exercise

Consider the following finite-state machine:

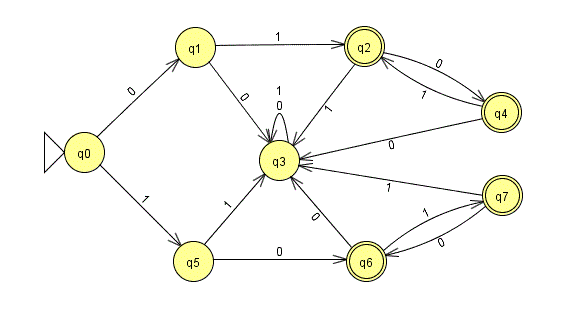
Which state is the start state?
Which state(s) are accepting states?
How many outgoing transitions does each state have? Is this required?
Which states(s) are “black hole” states – i.e., states that, once you enter them, you can never leave? Will you always need that type of state in your FSM? When is it useful?
Which of the following inputs are accepted by this FSM, and which are rejected?
- 0
- 10
- 111
- 010
- 101010
- 0100
How would you describe the inputs that are accepted by this FSM?
Would it be possible to simplify this FSM by reducing the number of states? If so, how? If not, why not?

Last updated on December 2, 2024.